Velocity of a particle varies as V=bx52 where b = 0.25 find work done by force from x = 0 to x = 4. Mass of particles is 500g
16J
32J
8J
12J
To solve the problem, we will use the work-energy theorem, which states that the work done by the net force on an object is equal to the change in its kinetic energy.
1. Identify the given parameters:
- Velocity of the particle: V=bx5/2 where b=0.25
- Mass of the particle: m=500g=0.5kg (convert grams to kilograms)
- Limits of integration for x: from xi=0 to xf=4
2. Calculate the initial and final velocities:
- Initial velocity at x=0:
Vi=b(0)5/2=0
- Final velocity at x=4:
Vf=b(4)5/2=0.25×45/2
To calculate 45/2:
45/2=(22)5/2=25=32
Therefore,
Vf=0.25×32=8m/s
3. Calculate the change in kinetic energy:
- The formula for kinetic energy is KE=12mv2.
- Initial kinetic energy KEi:
KEi=12mV2i=12×0.5×02=0
- Final kinetic energy KEf:
KEf=12mV2f=12×0.5×82=12×0.5×64=16J
4. Calculate the work done:
- According to the work-energy theorem:
W=KEf−KEi=16−0=16J
5. Final Answer:
- The work done by the force from x=0 to x=4 is 16J.
- Velocity of the particle: V=bx5/2 where b=0.25
- Mass of the particle: m=500g=0.5kg (convert grams to kilograms)
- Limits of integration for x: from xi=0 to xf=4
- Initial velocity at x=0:
Vi=b(0)5/2=0
- Final velocity at x=4:
Vf=b(4)5/2=0.25×45/2
To calculate 45/2:
45/2=(22)5/2=25=32
Therefore,
Vf=0.25×32=8m/s
- The formula for kinetic energy is KE=12mv2.
- Initial kinetic energy KEi:
KEi=12mV2i=12×0.5×02=0
- Final kinetic energy KEf:
KEf=12mV2f=12×0.5×82=12×0.5×64=16J
- According to the work-energy theorem:
W=KEf−KEi=16−0=16J
- The work done by the force from x=0 to x=4 is 16J.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Force on a particle varies with position (x) of particle as shown, calculate work done by force from x=0 to x=30 m.
 A5250JB4250JC7500JD3750J
A5250JB4250JC7500JD3750JA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
A12kx2B12kv2C12mv2D2mv2A force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
A−k2aB−kaC−2kaD−ak
Force acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionThe displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View SolutionThe velocity of a particle of mass 1 kg is given by v=10√x the work done by the forceacting on the particle during its motion from x=4 to x=9m is
View SolutionA body of mass 0.5kg travels in a straight line with velocity v=ax3/2 where a=5m/s2. The work done by the net force during its displacement from x=0 to x=2m is
View SolutionA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
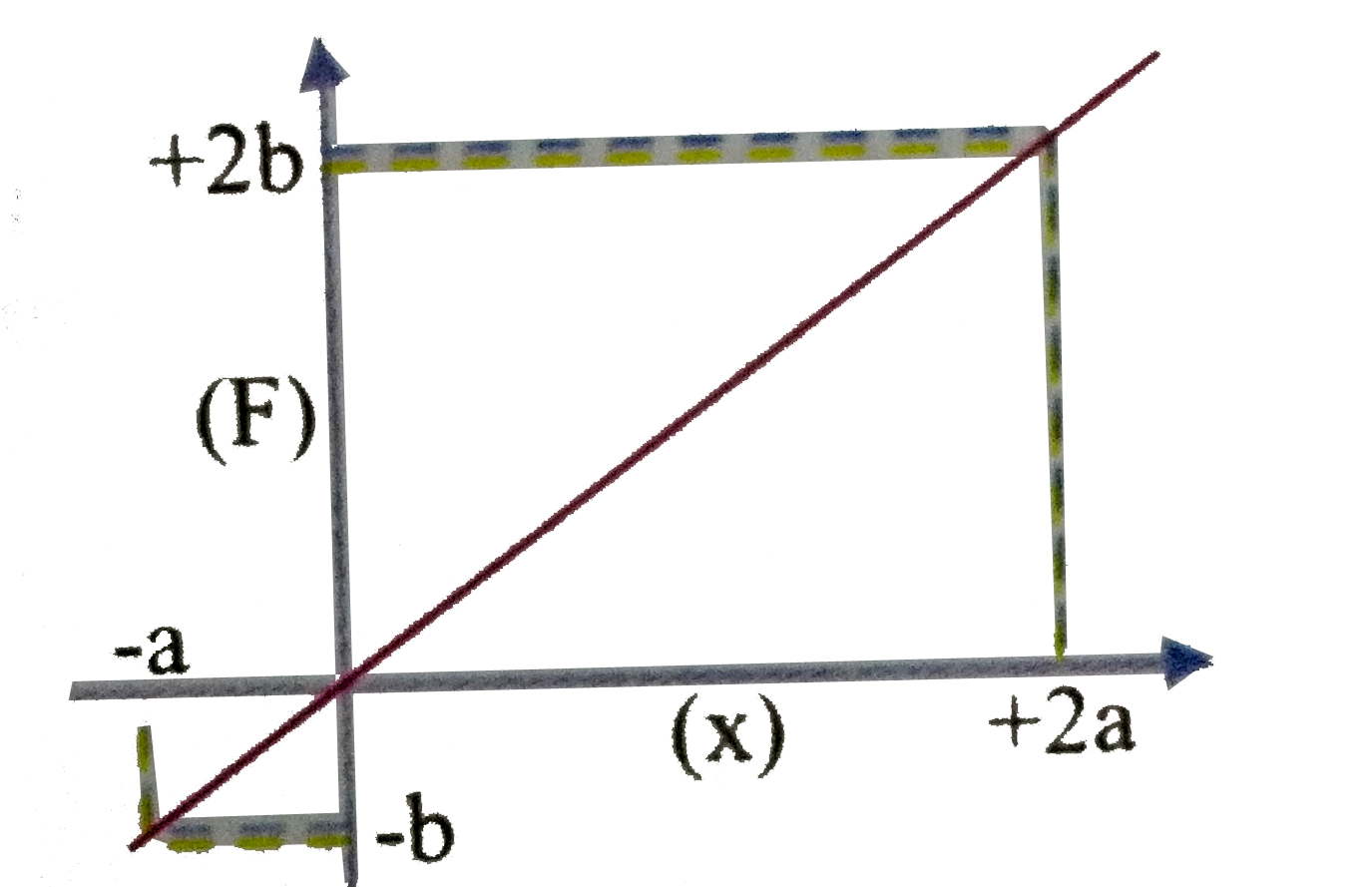 .
.
View Solution

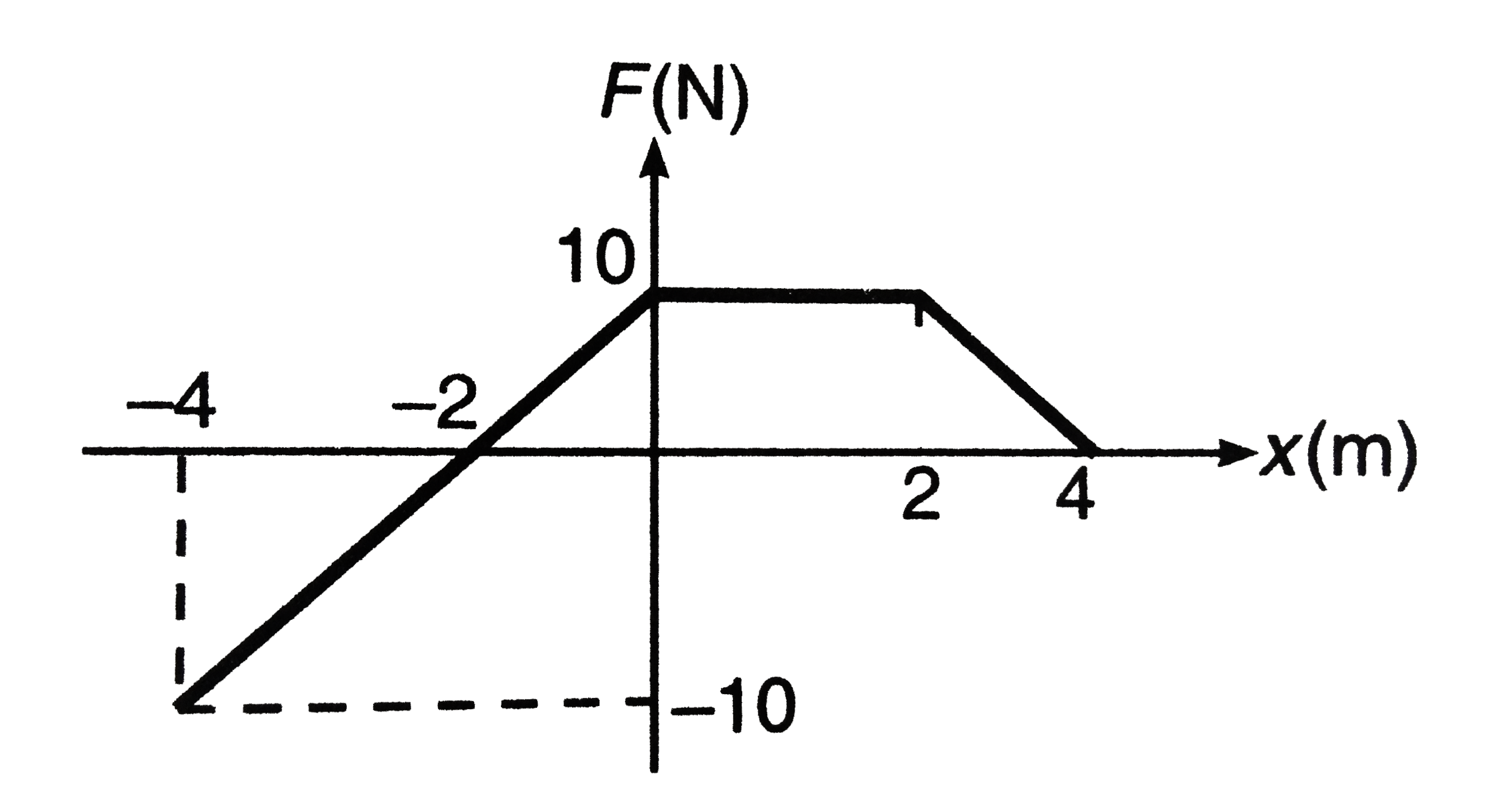 .
.