A small bulb is placed at the bottom of a tank containing water to a depth of √7 m . The refractive index of water is 43. The area of the surfacee of water through which light from the bulb cam emerge out is xπm2 . The value of x is ________.
To solve the problem, we need to determine the area of the surface of water through which light from a bulb at the bottom of a tank can emerge. The bulb is located at a depth of √7 m, and the refractive index of water is 43.
1. Identify the Depth of the Bulb:
The depth D of the bulb is given as:
D=√7 m
2. Determine the Critical Angle:
The critical angle θc can be calculated using Snell's law. The formula for the critical angle when light travels from a medium with a higher refractive index (water) to a medium with a lower refractive index (air) is:
sin(θc)=n2n1
where n1=43 (refractive index of water) and n2=1 (refractive index of air).
Thus,
sin(θc)=143=34
3. Calculate the Critical Angle:
Using the inverse sine function:
θc=sin−1(34)
4. Determine the Radius of the Circle of Light:
The radius r of the circle of light that can emerge from the water surface can be found using the relationship:
r=D⋅tan(θc)
Here, D=√7 m. To find tan(θc), we can use the triangle formed by the depth and the angles:
tan(θc)=oppositeadjacent=3√4=32
Therefore,
r=√7⋅32
5. Calculate the Area of the Circle:
The area A of the circle through which light can emerge is given by:
A=πr2
Substituting r:
A=π(√7⋅32)2=π(3√72)2=π⋅9⋅74=63π4 m2
6. Express the Area in the Required Form:
The area is given as xπ m². Thus, we can equate:
xπ=63π4
Dividing both sides by π:
x=634=15.75
Final Answer:
The value of x is 15.75.
The depth D of the bulb is given as:
D=√7 m
The critical angle θc can be calculated using Snell's law. The formula for the critical angle when light travels from a medium with a higher refractive index (water) to a medium with a lower refractive index (air) is:
sin(θc)=n2n1
where n1=43 (refractive index of water) and n2=1 (refractive index of air).
Thus,
sin(θc)=143=34
Using the inverse sine function:
θc=sin−1(34)
The radius r of the circle of light that can emerge from the water surface can be found using the relationship:
r=D⋅tan(θc)
Here, D=√7 m. To find tan(θc), we can use the triangle formed by the depth and the angles:
tan(θc)=oppositeadjacent=3√4=32
Therefore,
r=√7⋅32
The area A of the circle through which light can emerge is given by:
A=πr2
Substituting r:
A=π(√7⋅32)2=π(3√72)2=π⋅9⋅74=63π4 m2
The area is given as xπ m². Thus, we can equate:
xπ=63π4
Dividing both sides by π:
x=634=15.75
The value of x is 15.75.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics -Section A
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section A
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION A)
20 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
A small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? Refractive index of water is 1.33. [Consider the bulb to be a point source]
View SolutionA small bulb is placed at the bottom of a tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? (Refractive index of water is 1.33. (Consider the bulb to be a point source)
View Solution
Knowledge Check
A small bulb is placed at the bottom of a tank containing water to a depth of 80cm. What is the area of the bulb can emerge out? Refractive index of water is 1.33. (Consider the bulb to be a point source.)
A3.13 m2B1.43 m2C2.61m2D0.88m2A fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
ABird and image of fish is 9mBFish and image of is 12mCFish and image of bird is 8mDFish and image of bird is 10m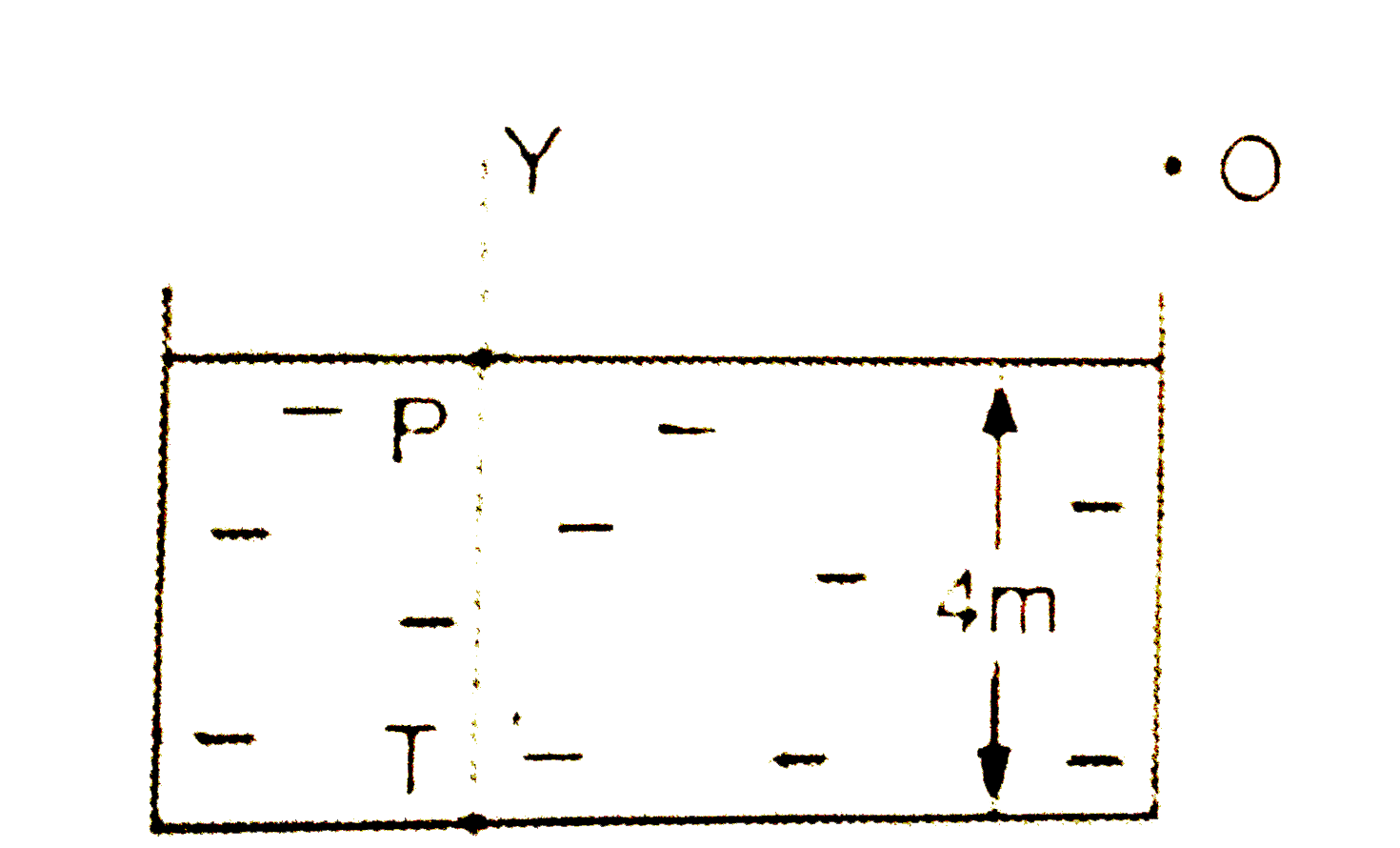
T is a point at the bottom of a tank filled with water, as shwon. The refractive index of water is 4/3. YPT is the vertical line through T. To an observer at the position O,T will appear to beAto the left of YTBsomewhere on YTCat a depth 3m below TDat a depth <3m below T
A small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from thr bulb can emerge. Take the value of refractive index of water to be 4/3.
View SolutionA small bulb (assumed to be a point source) is placed at the bottom of a tank containing water to a depth of 80cm. Find out the area of the surface of water through which light from thr bulb can emerge. Take the value of refractive index of water to be 4/3.
View SolutionWhat will be the speed of light in water if it is given that the refractive index of water is 4/3 and the speed of light in air is 3×108 m/s?
View SolutionWhat is the real depth of a swimming pool when its bottom appears to be raised by 1 m ? Given refractive index of water is 4/3.
View Solution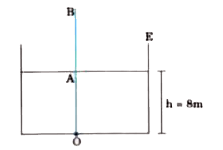
An object O is placed at the bottom of a container in which water is filled up to a height of 8m. Refractive index of water is 4/3. OAB is a vertical line. Observer is looking at O from point E as shown in figure. For the observer, position of O will appear to be
View Solution
