Question

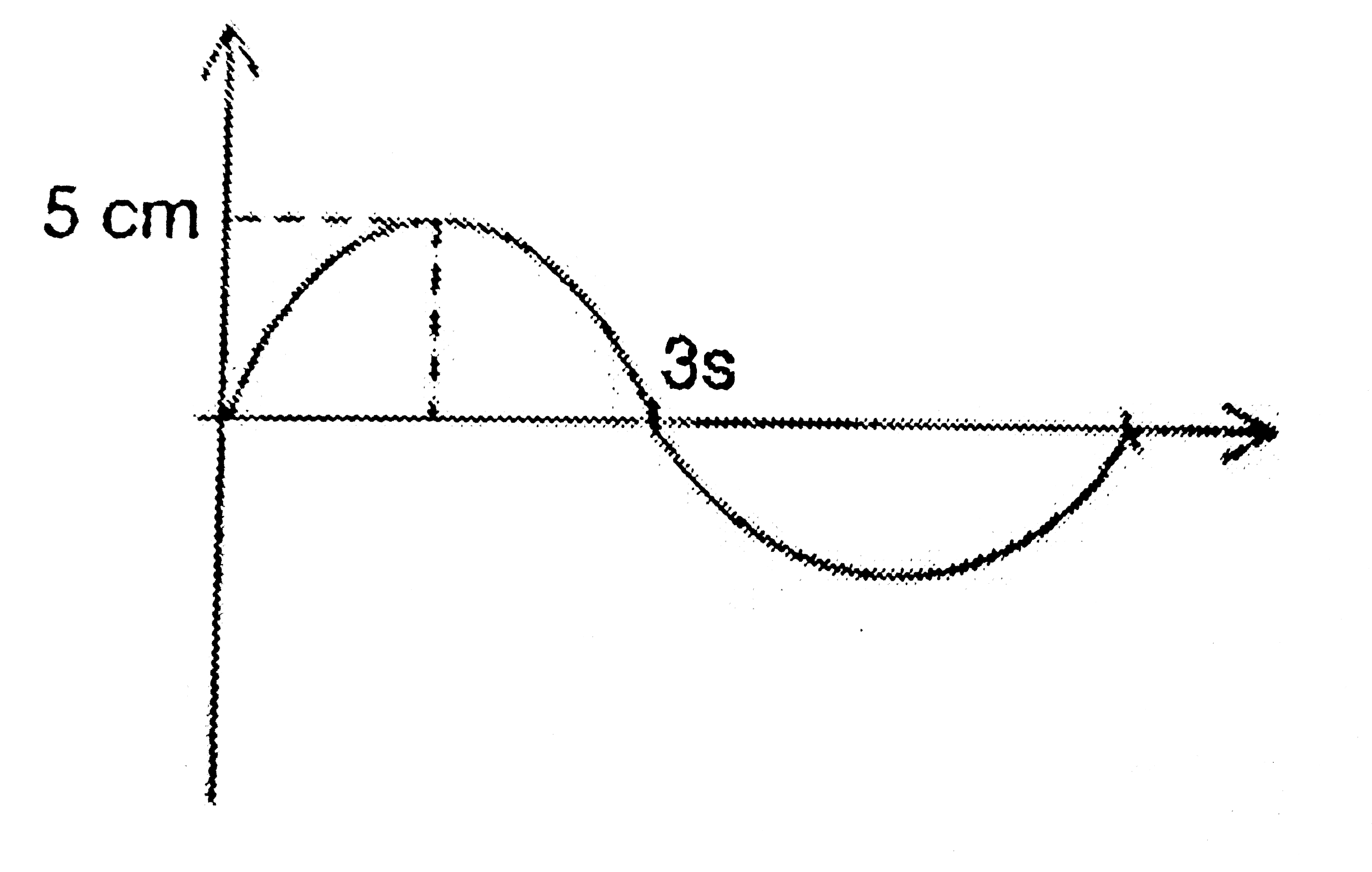
The motion of a simple pendulum executing S.H.M is represented by the following equation. $y=A\sin (\pi t+\varphi )$, where time is measured in second. The length of pendulum is

Options

A. 97.23cm
B. 25.3cm
C. 99.4cm
D. 406.1cm

Explanation

To find the length of the pendulum from the given equation of motion $$y=A\sin (\pi t+\varphi )$$, we can follow these steps:

Step 1: Identify the angular frequency
The equation of motion for a simple harmonic motion (SHM) is given by:
\( y = A \sin(\omega t + \phi) \)
From the given equation, we can see that the angular frequency \( \omega \) is equal to \( \pi \).

Step 2: Relate angular frequency to the length of the pendulum
For a simple pendulum, the angular frequency \( \omega \) is related to the length \( l \) of the pendulum and the acceleration due to gravity \( g \) by the formula:
\( \omega = \sqrt{\frac{g}{l}} \)
Substituting \( \omega = \pi \) into this equation gives:
\( \pi = \sqrt{\frac{g}{l}} \)

Step 3: Square both sides of the equation
To eliminate the square root, we square both sides:
\( \pi^2 = \frac{g}{l} \)

Step 4: Rearrange to solve for the length \( l \)
Now, we can rearrange the equation to solve for \( l \):
\( l = \frac{g}{\pi^2} \)

Step 5: Substitute the value of \( g \)
The acceleration due to gravity \( g \) is approximately \( 9.8 \, \text{m/s}^2 \). Substituting this value into the equation gives:
\( l = \frac{9.8}{\pi^2} \)

Step 6: Calculate \( \pi^2 \)
Calculating \( \pi^2 \) (where \( \pi \approx 3.14 \)):
\( \pi^2 \approx 3.14^2 \approx 9.8596 \)

Step 7: Calculate the length \( l \)
Now substituting \( \pi^2 \) back into the equation for \( l \):
\( l = \frac{9.8}{9.8596} \approx 0.994 \, \text{m} \)

Step 8: Convert to centimeters
To convert meters to centimeters, we multiply by 100:
\( l \approx 0.994 \, \text{m} \times 100 = 99.4 \, \text{cm} \)

Final Answer
Thus, the length of the pendulum is approximately \( 99.4 \, \text{cm} \).

---