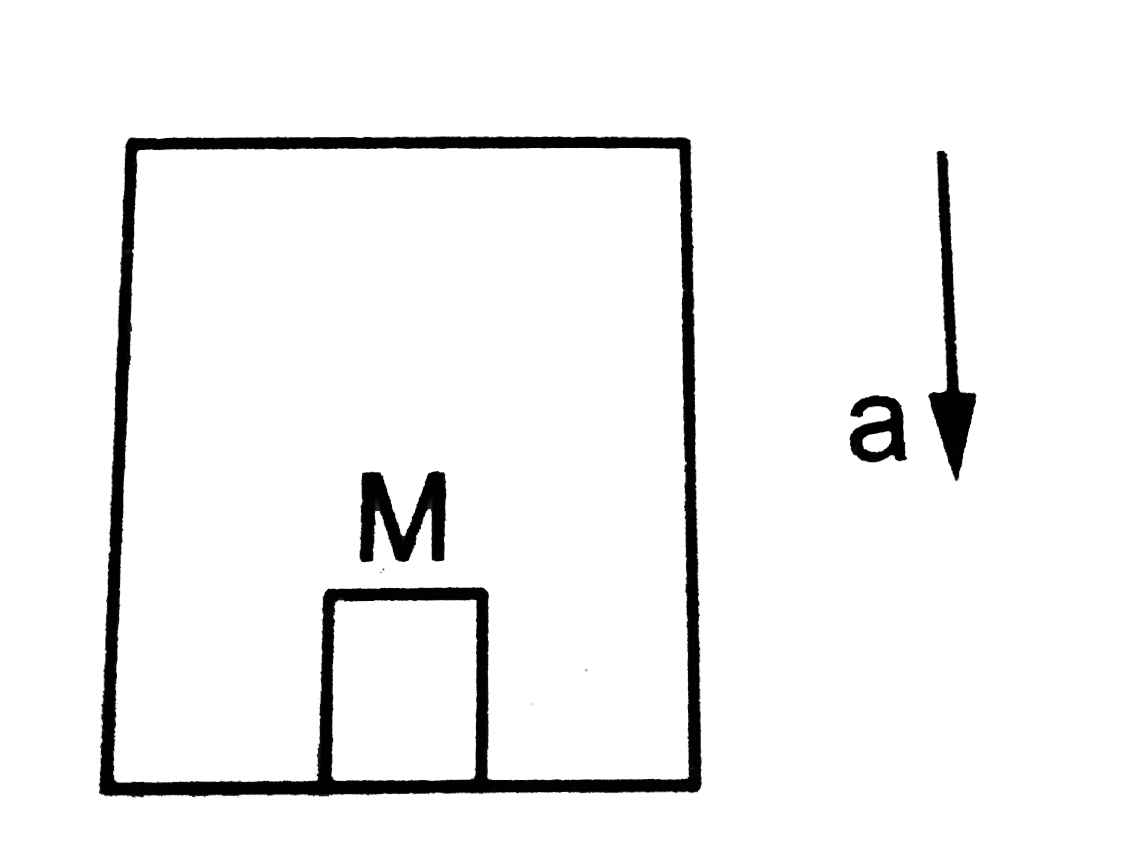
A block of mass M placed inside a box descends vertically with acceleration 'a'. The block exerts a force equal to one-fourth of its weight on the floor of the box. The value of 'a' will be
g4
g2
3g4
g
To solve the problem, we need to analyze the forces acting on the block of mass M that is placed inside a box descending with an acceleration a.
1. Identify the Forces Acting on the Block:
- The weight of the block W=Mg acts downward.
- The normal force N exerted by the floor of the box acts upward.
- Since the box is accelerating downwards, a pseudo force Fpseudo=Ma acts upwards on the block.
2. Set Up the Equation of Motion:
- In the non-inertial frame of the box, the net force acting on the block can be expressed as:
N−Mg+Ma=0
- Rearranging gives:
N=Mg−Ma
3. Use the Given Condition:
- According to the problem, the normal force N is equal to one-fourth of the weight of the block:
N=14Mg
4. Equate the Two Expressions for Normal Force:
- From the previous steps, we have:
Mg−Ma=14Mg
5. Solve for Acceleration a:
- Rearranging the equation gives:
Mg−14Mg=Ma
- Simplifying the left side:
34Mg=Ma
- Dividing both sides by M (assuming M≠0):
34g=a
6. Final Result:
- The value of the acceleration a of the box is:
a=34g
- The weight of the block W=Mg acts downward.
- The normal force N exerted by the floor of the box acts upward.
- Since the box is accelerating downwards, a pseudo force Fpseudo=Ma acts upwards on the block.
- In the non-inertial frame of the box, the net force acting on the block can be expressed as:
N−Mg+Ma=0
- Rearranging gives:
N=Mg−Ma
- According to the problem, the normal force N is equal to one-fourth of the weight of the block:
N=14Mg
- From the previous steps, we have:
Mg−Ma=14Mg
- Rearranging the equation gives:
Mg−14Mg=Ma
- Simplifying the left side:
34Mg=Ma
- Dividing both sides by M (assuming M≠0):
34g=a
- The value of the acceleration a of the box is:
a=34g
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section A
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B
10 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION B)
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
Knowledge Check
An elevator is moving vertically up with a acceleration a the force exerted on the floor by a passenger of mass m is
AmgBmaCmg - maDmg + maIn an elevator moving vertically up with an acceleration g, the force exerted on the floor by a passanger of mass M is
AMgB12MgCzeroD2 MgAn elevator is moving vertically up with a acceleration a the force exerted on the floor by a passenger of mass m is
A12mgBmgC2mgDZero
What should be the acceleration a of the box shown in figure so that the block of mass m exerts a force mg4 on the force of the box?

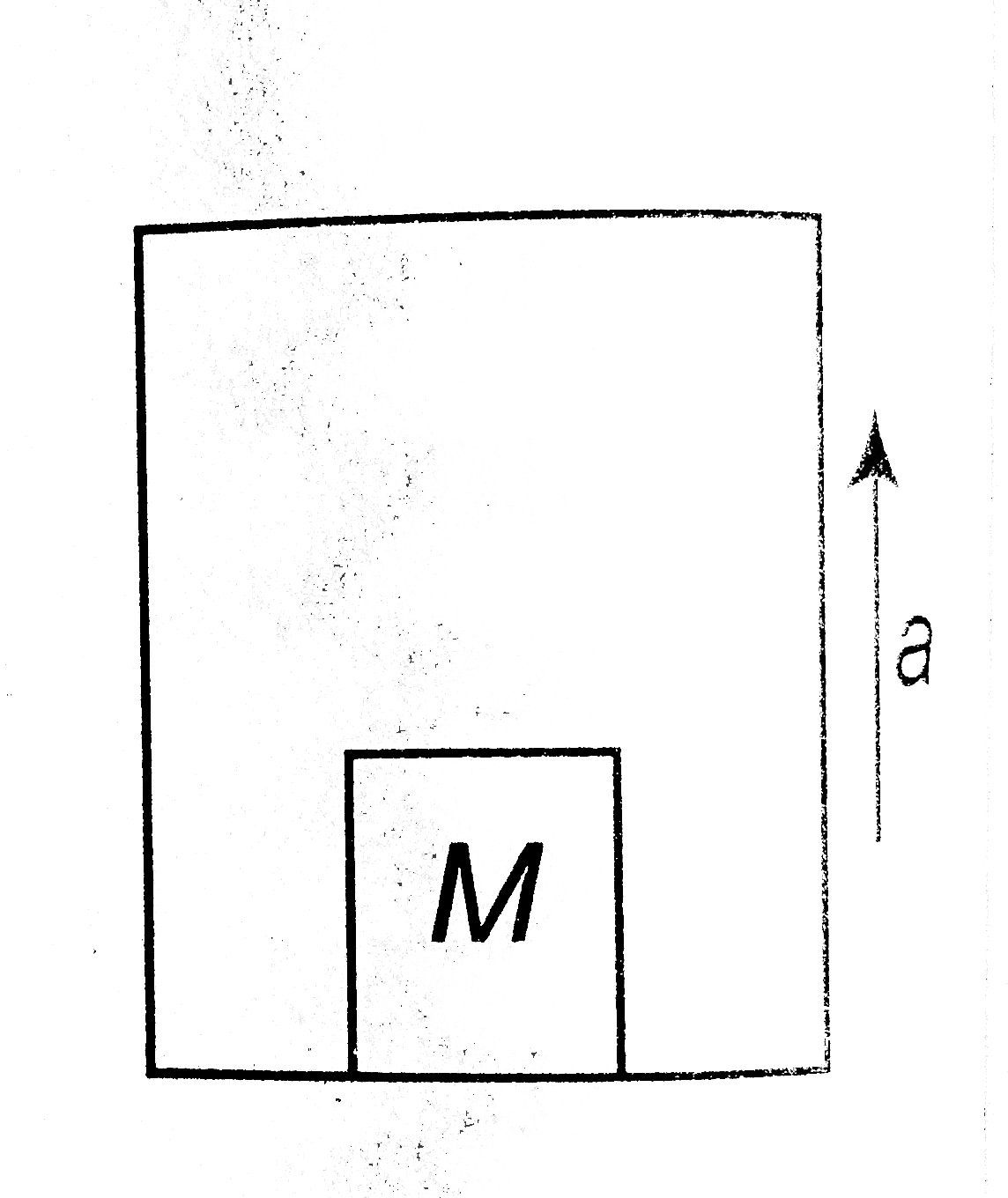
View SolutionWith what acceleration 'a' should the box of figure moving up so that the block of mass M exerts a force 7Mg/4 on the floor of the box?
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass 1 kg is placed on a horizontal surface . The reaction force to the weight of the block is
View SolutionA block of mass m is placed on a smooth wedge of inclination θ. The whole system is accelerated horizontally, so that the block does not slip on the wedge. The force exerted by the wedge on the block (g is acceleration due to gravity) will be
View Solution