A long straight wire with a circular cross-section having radius R, is carrying a steady current I. The current I is uniformly distributed across this cross-section. Then the variation of magnetic field due to current I with distance r (r
The correct Answer is:B
To find the variation of the magnetic field B due to a long straight wire carrying a steady current I with distance r from its center (for r<R), we can use Ampère's law.
1. Understand the Setup: We have a long straight wire with a circular cross-section of radius R carrying a steady current I. The current is uniformly distributed across the cross-section.
2. Use Ampère's Law: According to Ampère's law, the magnetic field B around a long straight current-carrying conductor can be calculated using the formula:
B⋅2πr=μ0Ienc
where Ienc is the current enclosed by the Amperian loop of radius r.
3. Calculate the Enclosed Current: Since the current is uniformly distributed, the current density J is given by:
J=IπR2
The current enclosed by a circular loop of radius r (where r<R) is:
Ienc=J⋅A=J⋅πr2=IπR2⋅πr2=Ir2R2
4. Substitute into Ampère's Law: Now substituting Ienc back into Ampère's law:
B⋅2πr=μ0Ir2R2
5. Solve for B: Rearranging the equation to solve for B:
B=μ0Ir2πR2
6. Conclusion: The magnetic field B inside the wire (for r<R) varies linearly with the distance r from the center of the wire:
B∝r
Final Answer:
The variation of the magnetic field B with distance r from the center of the wire (for r<R) is given by:
B=μ0Ir2πR2
B⋅2πr=μ0Ienc
where Ienc is the current enclosed by the Amperian loop of radius r.
J=IπR2
The current enclosed by a circular loop of radius r (where r<R) is:
Ienc=J⋅A=J⋅πr2=IπR2⋅πr2=Ir2R2
B⋅2πr=μ0Ir2R2
B=μ0Ir2πR2
B∝r
The variation of the magnetic field B with distance r from the center of the wire (for r<R) is given by:
B=μ0Ir2πR2
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PART : PHYSICS30videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)20videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B10videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )10videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question360videos
JEE MAINS 2023 JAN ACTUAL PAPER
Similar Questions
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 View Solution
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
A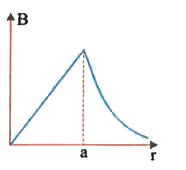 B
B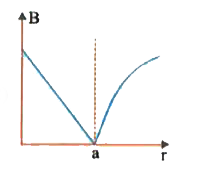 C
C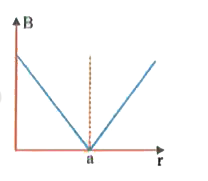 D
D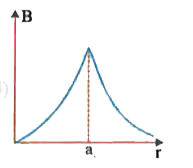
- Question 2 - Select One
A long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross section. The ratio of the magnetis field at (a)/(2)and(2a) is
A(1/2)B(1/4)C4D1 - Question 3 - Select One
A long straight wire of a circular cross section (radius a) carries a steady current 7 and the current / is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance from the centre of the wire?
A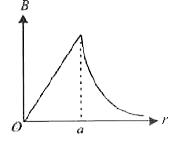 B
B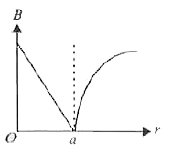 C
C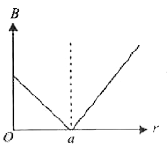 D
D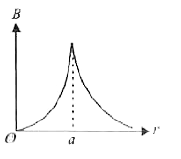
Figure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 View Solution
View SolutionFigure show a long straight wire of a circular a cross-section with radius 'a' carrying steady curent I. The curent I is uniformaly distributed across this c ross -section.Calclulate the magnetic field in the regionr1<aandr2> a.
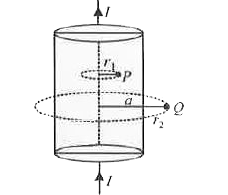 View Solution
View SolutionThe adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
 View Solution
View SolutionThe figure shows a long striaght wire of a circular cross-section (radius a) carrying steady current I.The current I is unifromly distributed across this distance a/2 and 2a from axis is
View Solution

