A uniform chain of 6 m length is placed on a table such that a part of its length is hanging over the edge of the table. The system is at rest. The co-efficient of static friction between the chain and the surface of the table is 0.5, the maximum length of the chain hanging from the table is _______________ m.
The correct Answer is:2
To solve the problem of finding the maximum length of a uniform chain that can hang over the edge of a table without slipping, we can follow these steps:
1. Understanding the Problem:
We have a uniform chain of total length L=6m. A part of this chain, denoted as x, is hanging over the edge of the table. The coefficient of static friction between the chain and the table is μ=0.5.
2. Weight of the Hanging Chain:
The weight of the hanging part of the chain (length x) can be expressed as:
Whanging=mL⋅x⋅g
where m is the total mass of the chain, g is the acceleration due to gravity, and mL is the mass per unit length.
3. Normal Force on the Table:
The normal force N acting on the part of the chain that is on the table (length L−x) is given by:
N=mL⋅(L−x)⋅g
4. Frictional Force:
The maximum static frictional force Ffriction that can act on the chain is:
Ffriction=μ⋅N=μ⋅(mL⋅(L−x)⋅g)
5. Setting Up the Equation:
For the chain to remain at rest, the frictional force must balance the weight of the hanging part:
Ffriction=Whanging
Substituting the expressions we derived:
μ⋅(mL⋅(L−x)⋅g)=mL⋅x⋅g
6. Canceling Common Terms:
We can cancel mL and g from both sides (assuming m and g are non-zero):
μ⋅(L−x)=x
7. Rearranging the Equation:
Rearranging gives:
μL−μx=x
μL=x+μx
μL=x(1+μ)
8. Solving for x:
We can now solve for x:
x=μL1+μ
9. Substituting Known Values:
Substitute μ=0.5 and L=6m:
x=0.5⋅61+0.5=31.5=2m
Final Answer:
The maximum length of the chain hanging from the table is 2m.
We have a uniform chain of total length L=6m. A part of this chain, denoted as x, is hanging over the edge of the table. The coefficient of static friction between the chain and the table is μ=0.5.
The weight of the hanging part of the chain (length x) can be expressed as:
Whanging=mL⋅x⋅g
where m is the total mass of the chain, g is the acceleration due to gravity, and mL is the mass per unit length.
The normal force N acting on the part of the chain that is on the table (length L−x) is given by:
N=mL⋅(L−x)⋅g
The maximum static frictional force Ffriction that can act on the chain is:
Ffriction=μ⋅N=μ⋅(mL⋅(L−x)⋅g)
For the chain to remain at rest, the frictional force must balance the weight of the hanging part:
Ffriction=Whanging
Substituting the expressions we derived:
μ⋅(mL⋅(L−x)⋅g)=mL⋅x⋅g
We can cancel mL and g from both sides (assuming m and g are non-zero):
μ⋅(L−x)=x
Rearranging gives:
μL−μx=x
μL=x+μx
μL=x(1+μ)
We can now solve for x:
x=μL1+μ
Substitute μ=0.5 and L=6m:
x=0.5⋅61+0.5=31.5=2m
The maximum length of the chain hanging from the table is 2m.
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PART : PHYSICS
30 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)
20 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B
10 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
A uniform chain of length l is placed on a rough table, with length l/3 hanging over the edge. If the chain just begins to slide off the table by itself from this portion, the coefficient of friction between the chain and the table is 1/K. Then find the value of K.
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?
View Solution
Knowledge Check
A chain is placed on a rough table, partially hanging, as shown in the figure. The coefficient of static friction between the chain and the table is μ = 0.4. If the maximum possible length of the hanging part is x and the length of the chain is L, then what is the value of Lx?
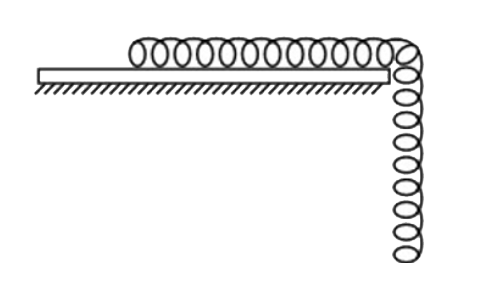 AμL1+μBμL1−μC(1−μ)L1+μDμL
AμL1+μBμL1−μC(1−μ)L1+μDμLA unifrom heavy chain is placed on a table with a part of it hanging over the edge. It just begins to slide when this part is one-third of its length. The coefficient of friction between the table and the chain is
A12B13C23D34A homogoneous chain of length L lies on a table. The coefficient of friction between the chain and the table is μ. The maximum length which can hang over the table in equilibrium is
A(μμ+1)LB(1−μμ)LC(1−μ1+μ)LD(2μ2μ+1)L
A uniform chain of length 2 m is kept on a table such that a length of 60 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg. What is the work done in pulling the entire chain on the table?
View SolutionA uniform chain of length l is placed on rough table with length l/n (where n>1) , hanging over the edge. If the chain just begins to slide off the table by itself from this position, the coefficient of friction between the chain and the table is
View SolutionA heavy uniform chain lies on horizantal table top. If the coefficient of friction between the chain and the table surface is 0.5, the maximum percentage of the length of the chain that can hang over one edge of the table is
View SolutionA heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.5, the maximum percentage of the length of the chain that can hang over one edge of the table is
View SolutionA heavy uniform chain lies on horizontal table top. If the coefficient of friction between the chain and the table surface is 0.25, the maximum percentage of the length of the chain that can hang over one edge of the table is
View Solution
