A block of mass 2 kg moving on a horizontal surface with speed of 4ms−1 enters a rough surface ranging from x = 0.5 m to x = 1.5 m. The retarding force in this range of rough surface is related to distance by F=−kx where k=12Nm−1. The speed of the block as it just crosses the rough surface will be :
zero
1.5ms−1
2.0ms−1
2.5ms−1
The correct Answer is:C
To solve the problem, we will use the work-energy principle. The work done by the retarding force will equal the change in kinetic energy of the block.
Step 1: Identify the initial conditions
The block has a mass m=2kg and an initial speed u=4m/s. The block enters the rough surface at x=0.5m and exits at x=1.5m.
Step 2: Determine the retarding force
The retarding force is given by:
F=−kx
where k=12N/m. Therefore, the force varies with position x.
Step 3: Calculate the work done by the retarding force
The work done W by the retarding force as the block moves from x=0.5m to x=1.5m is given by:
W=∫x2x1Fdx=∫1.50.5−kxdx
Substituting k=12:
W=∫1.50.5−12xdx
Step 4: Evaluate the integral
Calculating the integral:
W=−12(x22)1.50.5=−12((1.5)22−(0.5)22)
Calculating the squares:
=−12(2.252−0.252)=−12(2.25−0.252)=−12(22)=−12
Thus, the work done by the retarding force is W=−12J.
Step 5: Calculate the change in kinetic energy
The initial kinetic energy KEi is:
KEi=12mu2=12×2×(4)2=16J
Let v be the final speed of the block after crossing the rough surface. The final kinetic energy KEf is:
KEf=12mv2
According to the work-energy principle:
W=KEf−KEi
Substituting the values:
−12=12×2v2−16
This simplifies to:
−12=v2−16
Rearranging gives:
v2=4
Taking the square root:
v=2m/s
Final Answer
The speed of the block as it just crosses the rough surface is 2m/s.
---
The block has a mass m=2kg and an initial speed u=4m/s. The block enters the rough surface at x=0.5m and exits at x=1.5m.
The retarding force is given by:
F=−kx
where k=12N/m. Therefore, the force varies with position x.
The work done W by the retarding force as the block moves from x=0.5m to x=1.5m is given by:
W=∫x2x1Fdx=∫1.50.5−kxdx
Substituting k=12:
W=∫1.50.5−12xdx
Calculating the integral:
W=−12(x22)1.50.5=−12((1.5)22−(0.5)22)
Calculating the squares:
=−12(2.252−0.252)=−12(2.25−0.252)=−12(22)=−12
Thus, the work done by the retarding force is W=−12J.
The initial kinetic energy KEi is:
KEi=12mu2=12×2×(4)2=16J
Let v be the final speed of the block after crossing the rough surface. The final kinetic energy KEf is:
KEf=12mv2
According to the work-energy principle:
W=KEf−KEi
Substituting the values:
−12=12×2v2−16
This simplifies to:
−12=v2−16
Rearranging gives:
v2=4
Taking the square root:
v=2m/s
The speed of the block as it just crosses the rough surface is 2m/s.
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PART : PHYSICS30videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)20videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B10videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )10videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question360videos
JEE MAINS 2023 JAN ACTUAL PAPER
Similar Questions
A body of mass 2 kg moving on a horiontal surface with apeed vi=1ms−1 enters a rough patch ranging from x=0.5m to x=1.5m. If the body comes to rest after pussing the patch, then find the retarding force on the body.
View SolutionA block of mass m=1kg moving on a horizontal surface with speed vi=2ms−1 enters a rough patch ranging from x0.10m→x=2.01m. The retarding force Fr on the block in this range ins inversely proportional to x over this range
Fr=−kxfor0.1<x<2.01m
=0 for <0.1m and x>2.01m where k=0.5J. What is the final K.E. and speed vf of the block as it crosses the patch?View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m=1kg moving on a horizontal surface with speed vi=2ms−1 enters a rough patch ranging from x0.10m→x=2.01m. The retarding force Fr on the block in this range ins inversely proportional to x over this range
Fr=−kxfor0.1<x<2.01m
=0 for <0.1m and x>2.01m where k=0.5J. What is the final K.E. and speed vf of the block as it crosses the patch?A2m−1B1m−1C3m−1D0.5m−1 - Question 2 - Select One
A block of mass 70kg is kept on a rough horizontal surface (μ=0.4) . A person is trying to pull the block by applying a horizontal force, but the block is not moving. The net contact force exerted by the surface on the block is F , then:
AF=280NBF=754NCF=700ND700N≤F≤754N - Question 3 - Select One
A block of mass M is using on a rough horizontal surface. μR is the coefficient of kinetic friction between the block and the surface. What is the net force exerted by the surface on the block?
AMgBμMgCMg√1+μ2KDMg√1−μ2K
A block of mass m=1kg moving on a horizontal surface with speed vi=2ms−1 enters a rough patch ranging from x0.10m→x=2.01m. The retarding force Fr on the block in this range ins inversely proportional to x over this range
Fr=−kxfor0.1<x<2.01m
=0 for <0.1m and x>2.01m where k=0.5J. What is the final K.E. and speed vf of the block as it crosses the patch?View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
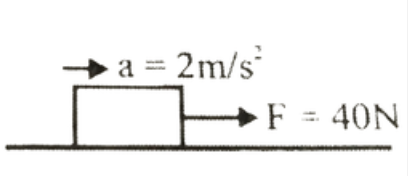 View Solution
View SolutionA block of mass "100gm" slides on a rough horizontal surface.If the speed of the block decreases from 10m/s to 5m/s ,the thermal energy developed in the process is
View SolutionA block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
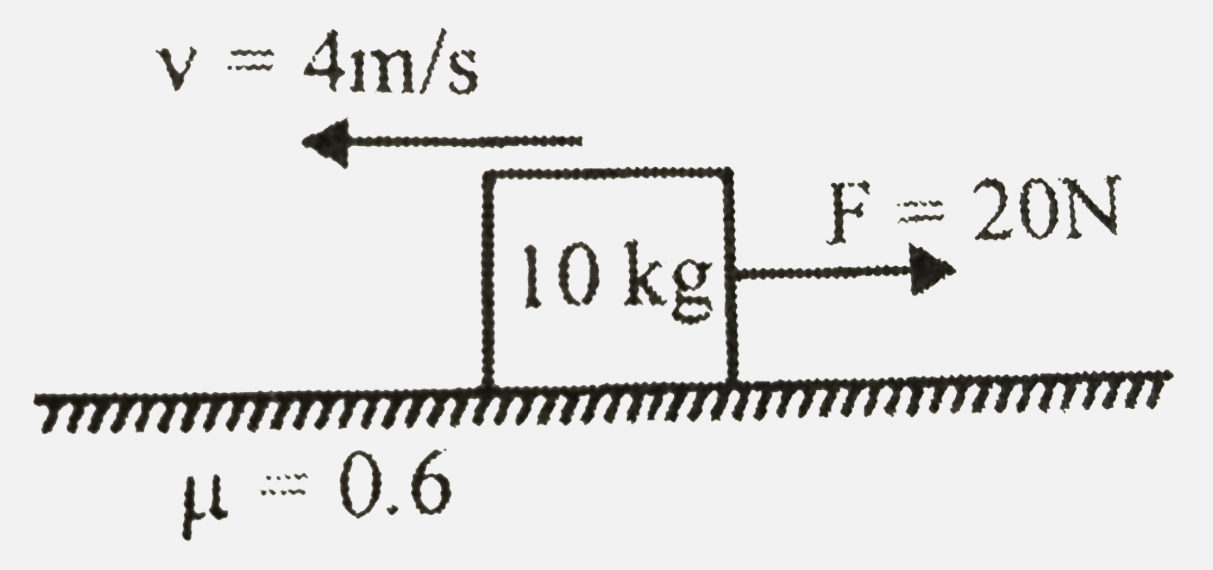 View Solution
View SolutionA block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
View Solution

