Velocity (v) and acceleration (a) in two systems of units 1 and 2 are related as v2=nm2v1anda2=a1mn respectively. Here m and n are constants. The relations for distance and time in two systems respectively are:
n3m3L1=L2andn2mT1=T2
L1=n4m2L2andT1=n2mT2
L1=n2mL2andT1=n4m2T2
n2mL1=L2andn4m2T1=T2
The correct Answer is:A
To solve this problem, we need to find the relations for distance and time between two systems of units given the relations for velocity and acceleration.
Given:
v2=nm2v1
a2=a1mn
Let's find the relations step-by-step.
Step 1: Finding the Relation for Time
1. Use the given relation for velocity:
v2=nm2v1
This implies:
v2v1=nm2
2. Use the given relation for acceleration:
a2=a1mn
This implies:
a2a1=1mn
3. Use the relation between velocity, acceleration, and time:
v=a⋅t
Therefore:
v2=a2⋅t2
v1=a1⋅t1
4. Divide the equations:
v2v1=a2⋅t2a1⋅t1
Substitute the known ratios:
nm2=1mn⋅t2t1
5. Solve for t2t1:
nm2=t2mn⋅t1
t2=n2m⋅t1
Step 2: Finding the Relation for Distance
1. Use the relation between velocity, distance, and time:
v=dt
Therefore:
d=v⋅t
2. Express distances in both systems:
d2=v2⋅t2
d1=v1⋅t1
3. Divide the equations:
d2d1=v2⋅t2v1⋅t1
4. Substitute the known ratios:
d2d1=(nm2)⋅(n2m)
5. Simplify:
d2d1=n3m3
d2=n3m3⋅d1
Final Relations:
- Time:
t2=n2m⋅t1
- Distance:
d2=n3m3⋅d1
v2=nm2v1
a2=a1mn
v2=nm2v1
This implies:
v2v1=nm2
a2=a1mn
This implies:
a2a1=1mn
v=a⋅t
Therefore:
v2=a2⋅t2
v1=a1⋅t1
v2v1=a2⋅t2a1⋅t1
Substitute the known ratios:
nm2=1mn⋅t2t1
nm2=t2mn⋅t1
t2=n2m⋅t1
v=dt
Therefore:
d=v⋅t
d2=v2⋅t2
d1=v1⋅t1
d2d1=v2⋅t2v1⋅t1
d2d1=(nm2)⋅(n2m)
d2d1=n3m3
d2=n3m3⋅d1
t2=n2m⋅t1
d2=n3m3⋅d1
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PART : PHYSICS30videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -A)20videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics-Section B10videos
JEE MAINS 2022
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )10videos
JEE MAINS 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question360videos
JEE MAINS 2023 JAN ACTUAL PAPER
Similar Questions
In two systems of relations among velocity , acceleration , and force are , respectively , v2=α2βv1,a2=αβa1,andF2=F1αβ. If αandβ are constants , then make relations among mass , length , and time in two systems.
View SolutionThe velocity, acceleration and force in two systems of units are related as under:
(i) v'=α2βv
(ii) a'=(αβ)a
(iii) F'=(1αβ)F
All the primed symbols belong to one system and unprimed ones belong to the other system. Here αandβ are dimensionless constants. Which of the following is/are correct?View Solution
Knowledge Check
- Question 1 - Select One
The numerical values and units of a physical quantity in two different system of units are n1,n2andu1,u2 respectively. Then
An1u2=n2u1Bn1u21=n2u22Cn1=n2&u1=u2Dn1u1=n2u2 - Question 2 - Select One
In given system a1anda2 are the accelerations of blocks 1 and 2. Then constraint relation is
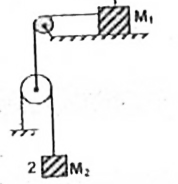 A2a1=a2B2a2=a1Ca1=a2Da1=4a2
A2a1=a2B2a2=a1Ca1=a2Da1=4a2 - Question 3 - Select One
Find the relation between acceleration a1 and a2
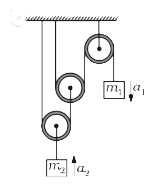 Aa1=2a2Ba1=4a2Ca1=a2Da1=3a2
Aa1=2a2Ba1=4a2Ca1=a2Da1=3a2
In two systems of units the relation between velocity acceleration and force is given by v2=v1ε2τ,a2=a1ετ,F2=F1ετ, where ε and τ constants then find in this new system:
(a) m2m1 , (b) L2L1View SolutionThe velocity of a particle in S.H.M. at positions x1 and x2 are v1 and v2 respectively. Determine value of time period and amplitude.
View SolutionIn the adjoining figure velocities and acceleration of the blocks 1 and 3 at any instant are v1=6m/s upwards ,a1=6m/s2 ( downwards ) and v3=3m/s ( upwards) ,a3=4ms2 ( downward) respectively. Find the velocity and the acceleration of the block 2 at that instant.
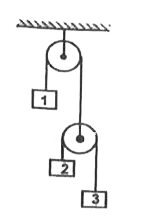 View Solution
View SolutionTwo cars of same mass are moving with velocities v1andv2 respectively. If they are stopped by supplying same breaking power in time t1andt2 respectively then v1v2 is
View SolutionIn a magnetic field as shown, in Fig. two horizontal wires of same mass and length l1andl2 are free to slide on different vertical rails with velocities v1andv2 respectively. If the resistance of two circuits are same and a1anda2 are acceleration of two horizontal wires respectively, the condition for a1>a2 is
 View Solution
View Solution

