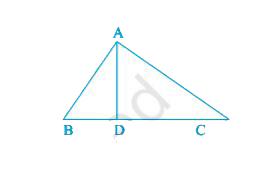
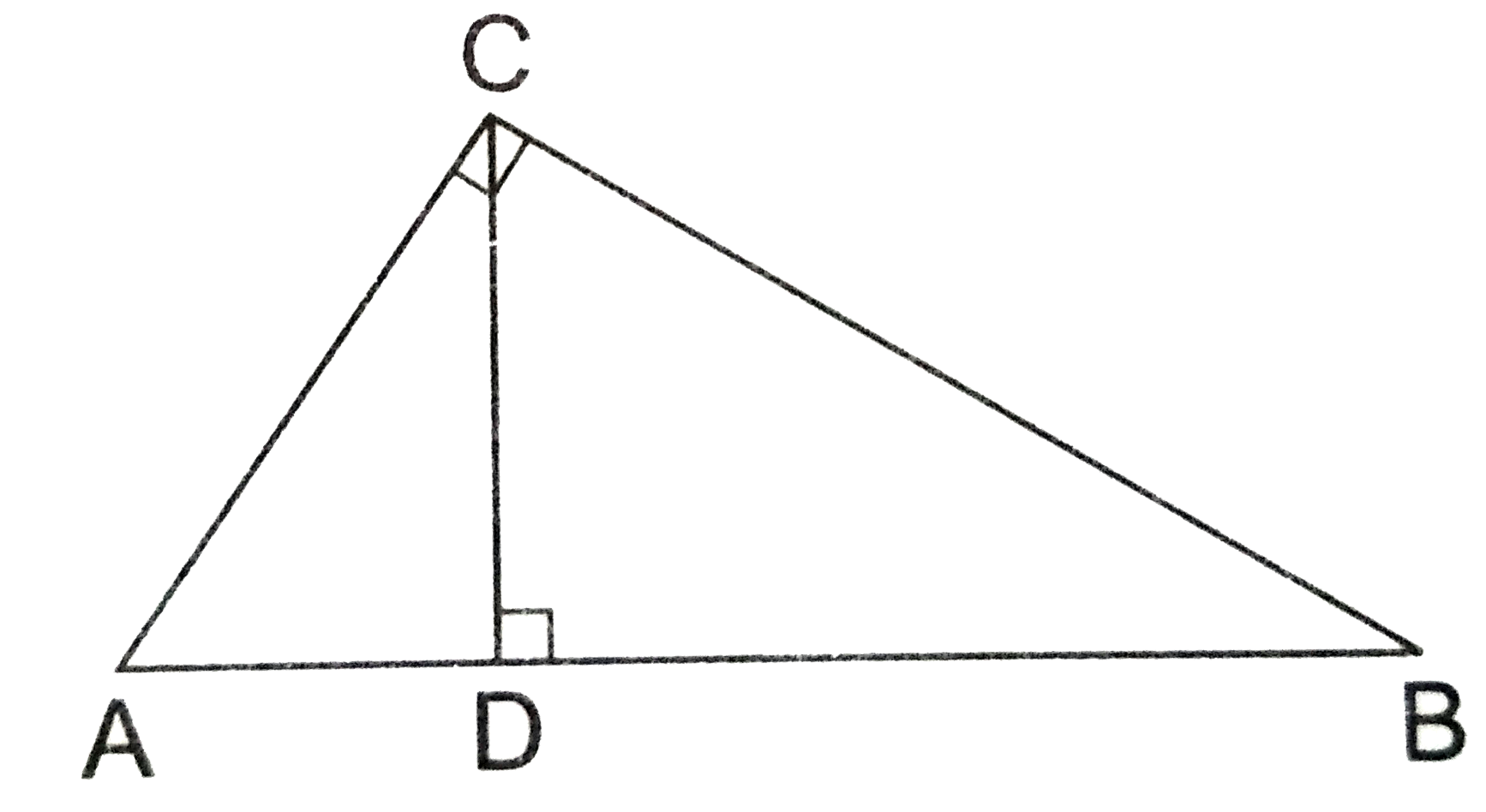
In Fig. ∠BAC=90∘andAD⊥BC. Then,

A
BD.CD=BC2
B
AB.AC=BC2
C
BD.CD=AD2
D
AB.AC=AD2
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Very Short Answer Type Questions
12 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Assertion and Reasoning Based Questions
2 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - BOARD CORNER (LONG SHORT ANSWER TYPE QUESTION ( 4 MARK EACH ))
4 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
Knowledge Check
In the figure given below ∠BAC=90∘ and AD ⊥ BC. Then
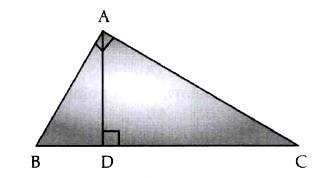 ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2
ABC×CD=AC2BAB×AC=BC2CBD×CD=AD2DAB×AC=AD2In the figure, if ∠BAC=90∘ and AD⊥BC, then:
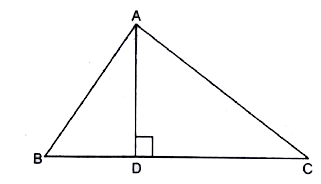 ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2In triangle ABC, ∠BAC=90∘ and AD⊥BC Such that ∠OBA=∠DAC Then:
ABD.CD=BC2BAB.AC=BC2CBD.CD=AD2DAB.AC=AD2
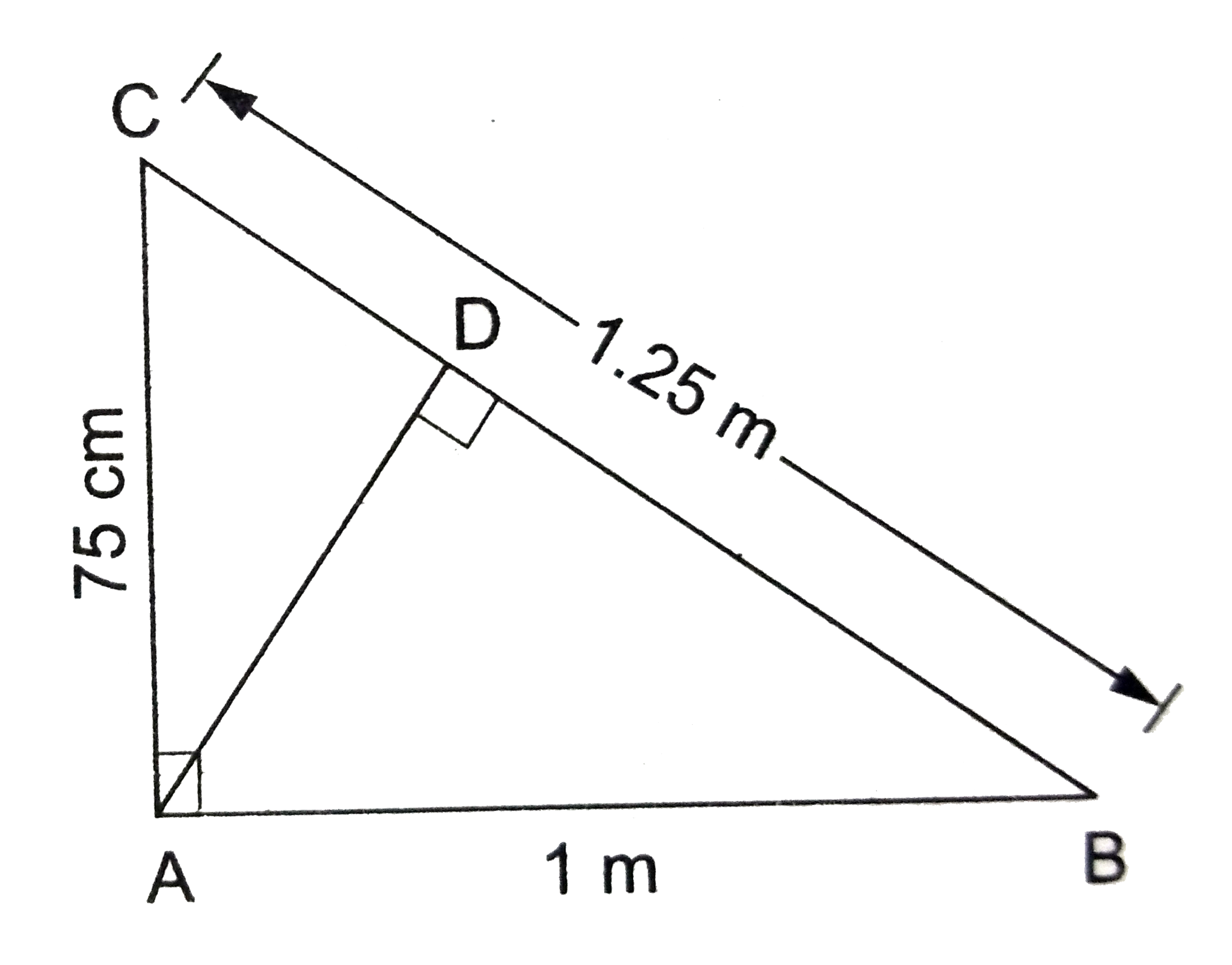
in the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.

View Solutionin the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.

View SolutionIn the given figure, ∠CAB=90∘andAD⊥BC. Show that ΔBDA~ΔBAC. if AC=75cm,AB=1mandBC=1.25cm, find AD.
View SolutionIn the given figure ∠ABC=90∘andCD⊥AB. Prove that BC2AC2=BDAD
View SolutionIn triangle ABC, ∠BAC=90∘andAD⊥BC. If BD = 3 and CD = 4 cm, then the length of AD is.
View Solution