In ΔABC, D and E are mid-points of AC and BC respectively such that DE || AB. If AD=2x,BE=2x−1,CD=x+1andCE=x−1, then find the value of x.
Text Solution
The correct Answer is:13
|
Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Assertion and Reasoning Based Questions
2 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Case Based Questions
12 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions
14 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
In ΔABC, D and E are points on sides AB and AC respectively such that DE∣∣BC. If AE=1.8cm, BD= 7.2cm and CE= 5.4cm, then the length of AD is
View SolutionIn the given figure of △ABC, D and E are points on CA and CB respectively such that DE || AB, AD = 2x, DC = x + 3, BE = 2x – 1, CE = x find x.
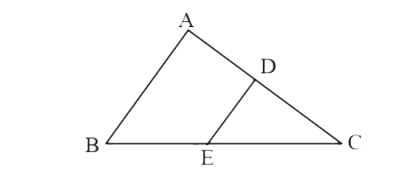
View Solution
Knowledge Check
In ΔABC D and E are points on sides AB and AC, such that DE || BC. If AD = x,DB = x - 2, AE = x + 2 and EC = x-1 then the value of x is
A4B2C1D8In ΔABC, DE || BC. If AD = 2x - 1, AE = 2x + 5, BD = x - 3 and CE = x - 1, then the value of x is:
A8B9C10D11A sum of money lent at compound interest for 2 years at 20% per annum would fetch Rs 482 more, if the interest was payable half-yearly than if it was payable annually. The sum is: (a) Rs 10,000 (b) Rs 20,000 (c) Rs 40,000 (d) Rs 50,000
AA. 30000BB. 20000CC. 10000DD.50000
In the figure ΔABC,DE∣∣AB. If AD=2x,DC=x+3,BE=2x−1CE=x then find the value of x.
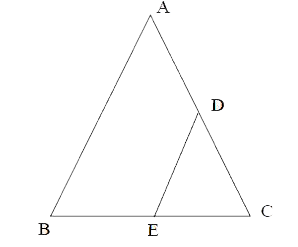
View SolutionIn a ΔABC,DE∣∣BC , the find the value of x.
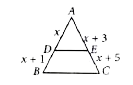
View SolutionIn Figure, DEBC, if AD=x,DB=x−2,AE=x+2 and EC=x−1, find the value of x.
View SolutionIn figure , DE∣∣BC.If AD=x+1 , DB = x-2 , AE =x+2andEC =x+3 , find the value of x .
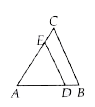
View SolutionIn a ΔABC,DandEare points on AC and BC respectively, AB and DE are perpendicular to BC. If AB=9cm,DE=3cmandAC=24cm, then AD is :
View Solution
