A potentiometer wire of length 1.0 m has a resistance of 10Ω. It is connected to a 6 V battery in seried with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40 cm.
To solve the problem step by step, we will determine the EMF of the primary cell that gives a balance point at 40 cm on a potentiometer wire.
Step 1: Understand the Circuit Setup
We have a potentiometer wire of length 1.0 m (100 cm) with a resistance of 10 Ω. It is connected to a 6 V battery in series with a resistance of 5 Ω.
Step 2: Calculate Total Resistance
The total resistance in the circuit (R_total) is the sum of the resistance of the potentiometer wire (R_p) and the series resistance (R_s):
Rtotal=Rp+Rs=10Ω+5Ω=15Ω
Step 3: Calculate Current in the Circuit
Using Ohm's law, we can find the current (I) flowing through the circuit:
I=VRtotal=6V15Ω=25A=0.4A
Step 4: Calculate the Potential Drop Across the Potentiometer Wire
The potential drop (V_p) across the potentiometer wire can be calculated using Ohm's law:
Vp=I×Rp=(25A)×10Ω=4V
Step 5: Determine the Potential Gradient
The potential gradient (k) is the potential drop per unit length of the potentiometer wire:
k=VpL=4V1.0m=4V/m
Step 6: Use the Balance Point to Find EMF of the Primary Cell
The balance point is at 40 cm (0.4 m). The EMF (E) of the primary cell can be calculated using the potential gradient:
E=k×length at balance point=4V/m×0.4m=1.6V
Conclusion
The EMF of the primary cell that gives a balance point at 40 cm is 1.6 V.
---
We have a potentiometer wire of length 1.0 m (100 cm) with a resistance of 10 Ω. It is connected to a 6 V battery in series with a resistance of 5 Ω.
The total resistance in the circuit (R_total) is the sum of the resistance of the potentiometer wire (R_p) and the series resistance (R_s):
Rtotal=Rp+Rs=10Ω+5Ω=15Ω
Using Ohm's law, we can find the current (I) flowing through the circuit:
I=VRtotal=6V15Ω=25A=0.4A
The potential drop (V_p) across the potentiometer wire can be calculated using Ohm's law:
Vp=I×Rp=(25A)×10Ω=4V
The potential gradient (k) is the potential drop per unit length of the potentiometer wire:
k=VpL=4V1.0m=4V/m
The balance point is at 40 cm (0.4 m). The EMF (E) of the primary cell can be calculated using the potential gradient:
E=k×length at balance point=4V/m×0.4m=1.6V
The EMF of the primary cell that gives a balance point at 40 cm is 1.6 V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (A. MULTIPLE CHOICE QUESTIONS WITH ONLY ONE CORRECT ANSWER)
36 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Objective Type Questions (MULTIPLE CHOICE QUESTIONS) (B. MULTIPLE CHOICE QUESTION FOR COMPETITIVE EXAMINATIONS)
20 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - REVISION EXERCISES (LONG ANSWER QUESTIONS)
10 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A potentiometer wire of length 1 m has a resistance of 10 Ω . It is connected to a 6 V battery in series with a resistance of 5 Ω . Determine the emf of the primary cell which gives a balance point at 40 cm.
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View Solution
Knowledge Check
A potentiometer wire has a length 2 m and resistance of 10Ω. It is coonnected in series with a resistance of 990Ω and a cell of e.m.f. 2 V. The potential gradient along the wire is
A0.01V/mB0.02V/mC0.03V/mD0.025V/mA potentiometer wire has length 10m and resistance 10Ω. It is connected to battery of EMF 11 volt and internal resistance 1Ω, then the potential gradient in the wire is
A10V/mB1V/mC0.1V/mDnone
A potentiometer wire of length 1 m has a resistance of 10Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View SolutionA potentiometer wire of length 1 m has a resistance of 100Ω. It is connected to a 6V battery in series with a resistance of 5Ω. Determine the emf of the primary cell which gives a balance point at 40cm.
View SolutionA potentiometer wire of length 1 m has a resistance of 5Ω. It is connected to a 8 V battery in series with a resistance of 15Ω. Determine the emf of the primary cell which gives a balance point at 60 cm.
View SolutionA potentiometer wire of length 1.0 m has a resistance of 15 ohm. It is connected to a 5 V source in series with a resistance of 5Ω. Determine the emf of the primary cell which has a balance point at 60 cm.
View SolutionA potentiometer wire of length 100 cm has a resistance of 10Ω. It is connected in series with a resistance R and cell of emf 2V and of of 40cm of the potentiometer wire. What is the value of R?
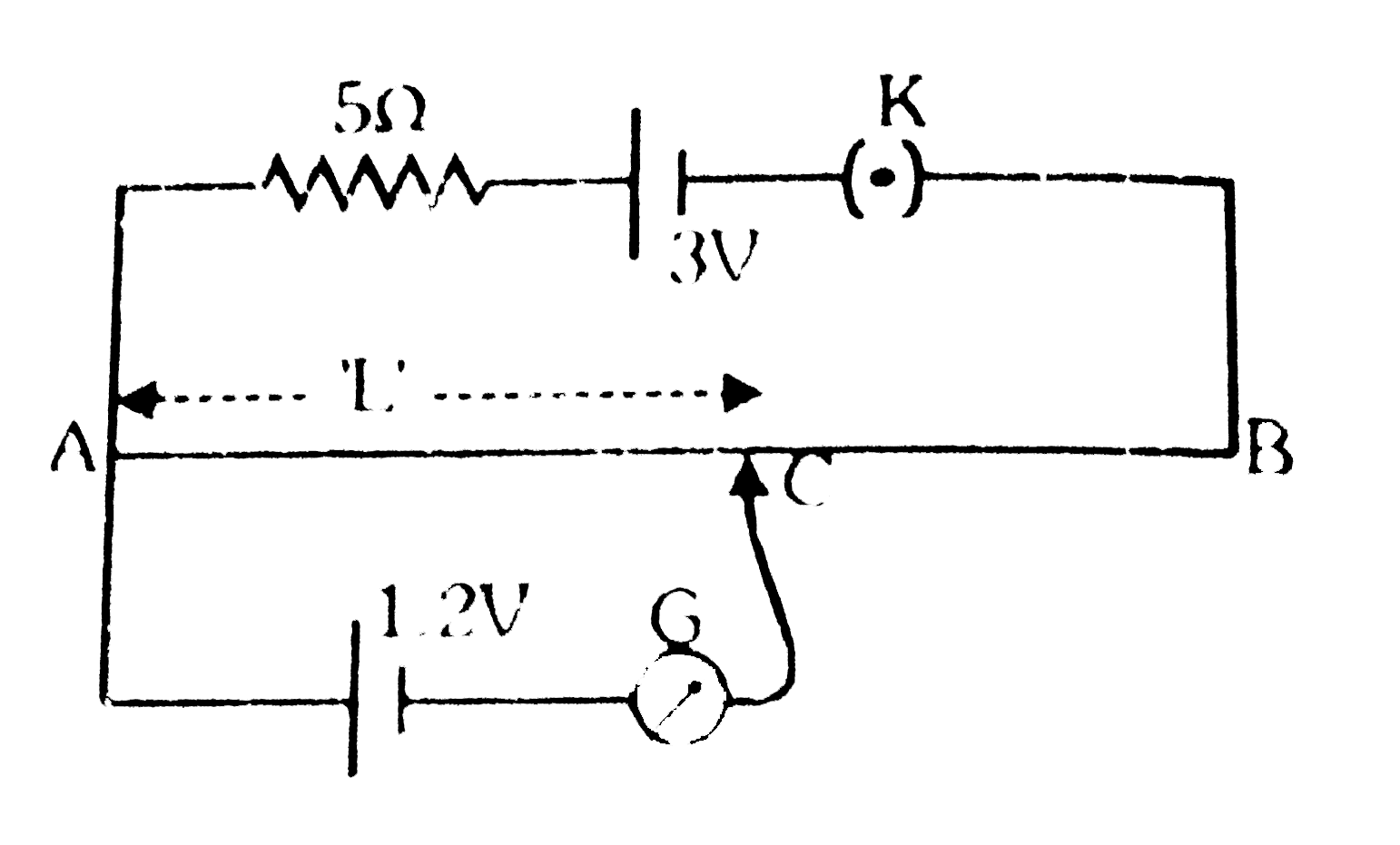
View SolutionThe potentiometer wire of length 100cm has a resistance of 10Ω. It is connected in series with a resistance of 5Ω and an accumulaot or emf 3V having negligible resistance. A source 1.2V is balanced against a length 'L' of the potentionmeter wire. find the value of L.
View Solution
