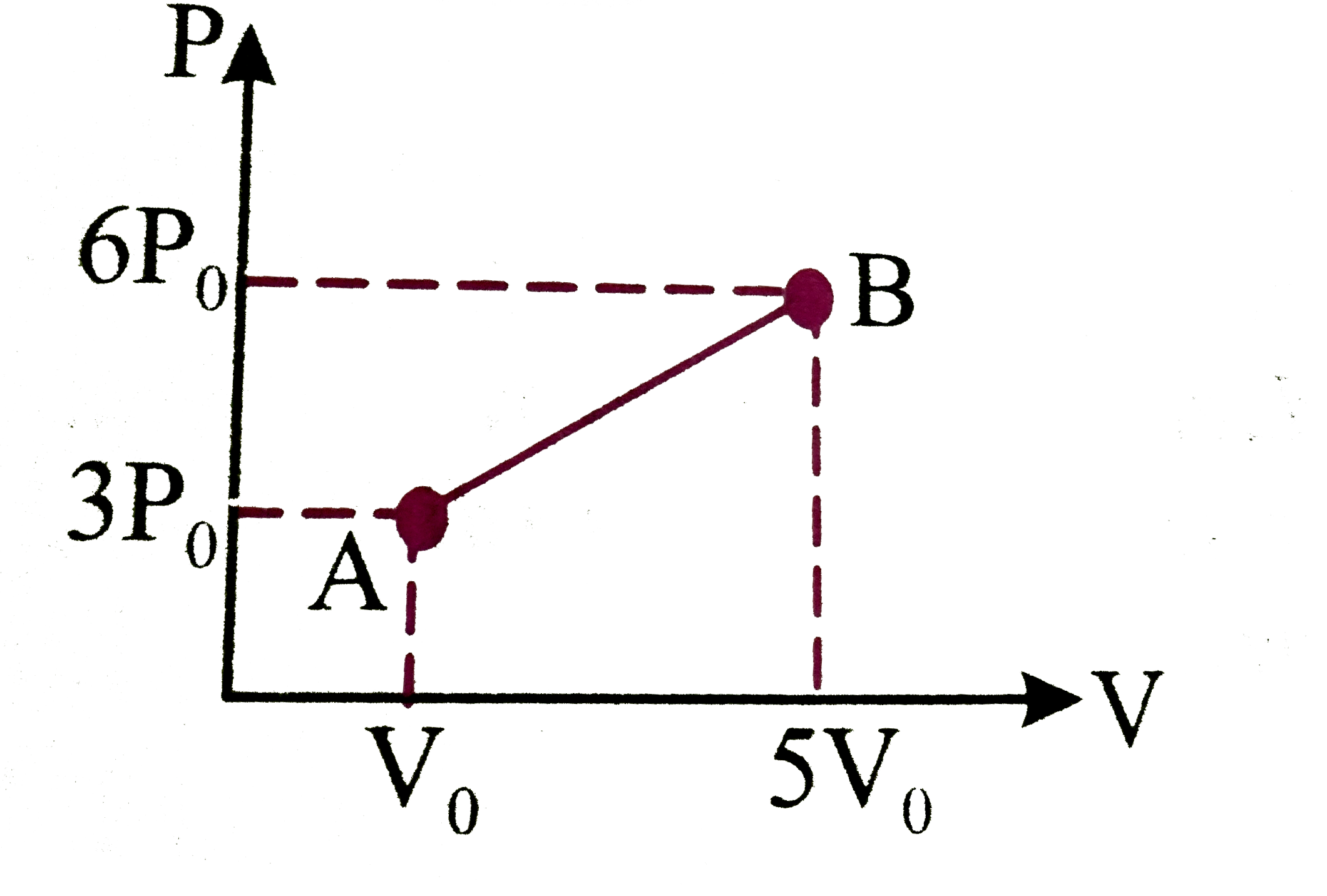
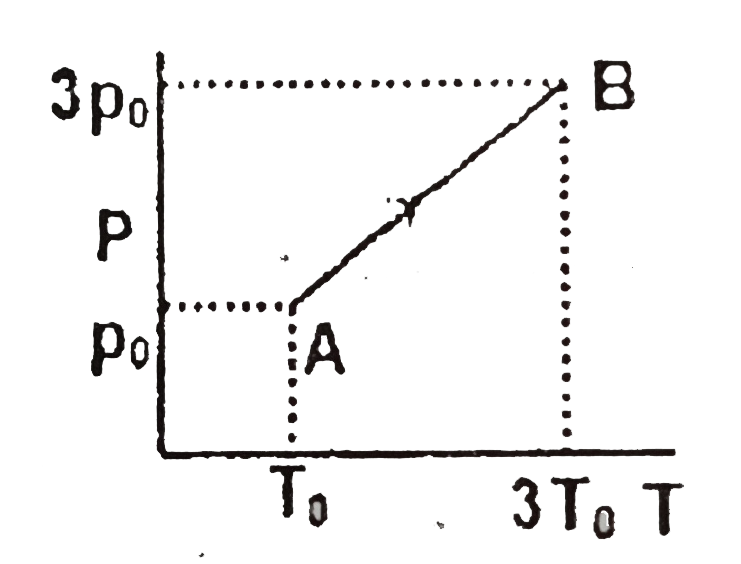
7 moles of monoatomic gas undergoes temperature charge of 40K. Find δ(U)
3500J
3000J
4000J
4500J
To find the change in internal energy (ΔU) of a monoatomic gas, we can use the formula:
ΔU=32nRΔT
Where:
- n = number of moles of the gas
- R = universal gas constant
- ΔT = change in temperature
1. Identify the given values:
- Number of moles (n) = 7 moles
- Change in temperature (ΔT) = 40 K
- For a monoatomic gas, the degrees of freedom (F) = 3
2. Use the universal gas constant (R):
- The value of R in joules per mole per kelvin is approximately 8.314J/(mol⋅K).
3. Substitute the values into the formula:
ΔU=32nRΔT
ΔU=32×7×8.314×40
4. Calculate ΔU:
- First, calculate 7×8.314:
7×8.314=58.198
- Then, multiply by 40:
58.198×40=2327.92
- Finally, multiply by 32:
ΔU=32×2327.92=3491.88J
5. Final Result:
ΔU≈3491.88J
- n = number of moles of the gas
- R = universal gas constant
- ΔT = change in temperature
- Number of moles (n) = 7 moles
- Change in temperature (ΔT) = 40 K
- For a monoatomic gas, the degrees of freedom (F) = 3
- The value of R in joules per mole per kelvin is approximately 8.314J/(mol⋅K).
ΔU=32nRΔT
ΔU=32×7×8.314×40
- First, calculate 7×8.314:
7×8.314=58.198
- Then, multiply by 40:
58.198×40=2327.92
- Finally, multiply by 32:
ΔU=32×2327.92=3491.88J
ΔU≈3491.88J
Topper's Solved these Questions
Similar Questions
Knowledge Check
One moles of an ideal monoatomic gas undergo the state change as shown in following graph (ln 2 = 0.7)
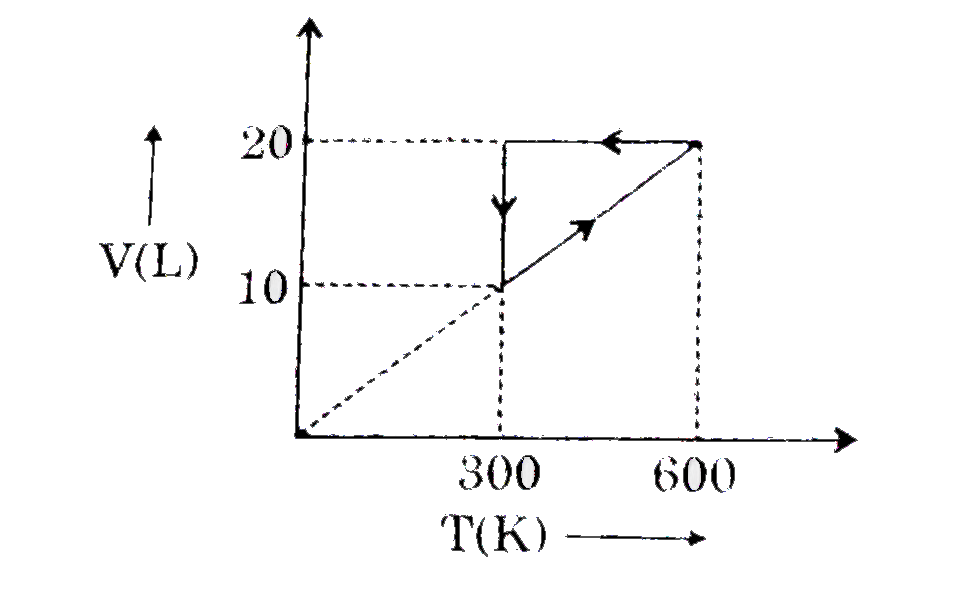
Efficiency of the cycle will be :A50%B25%C13.63%D12%One moles of an ideal monoatomic gas undergo the state change as shown in following graph (ln 2 = 0.7)
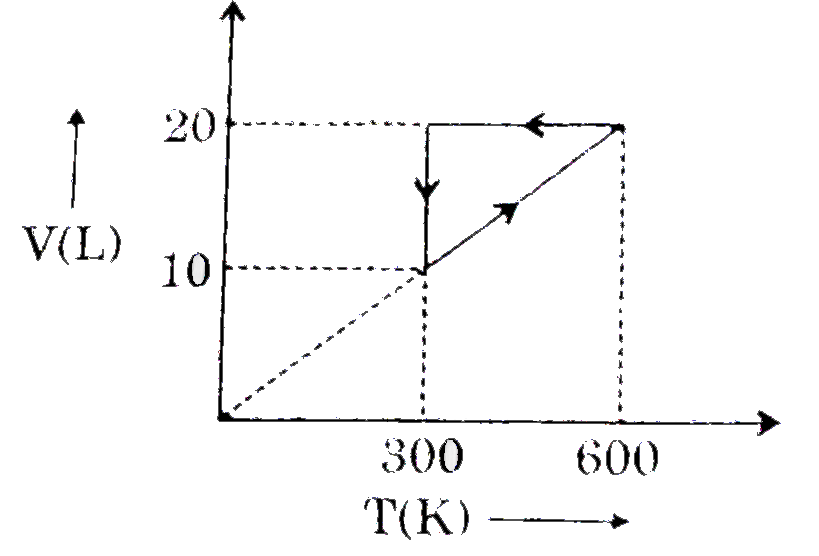
Correct graph for the process in paragraph is:A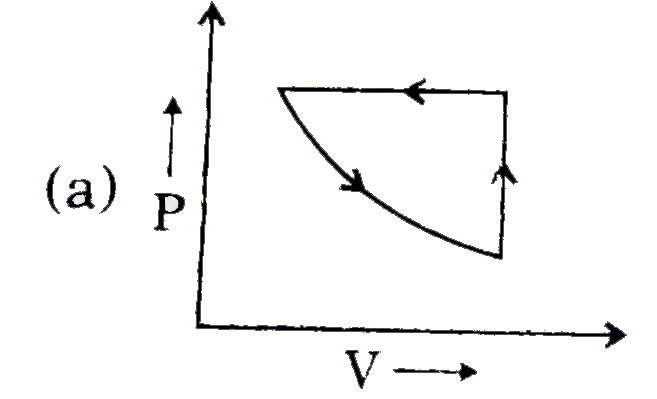 B
B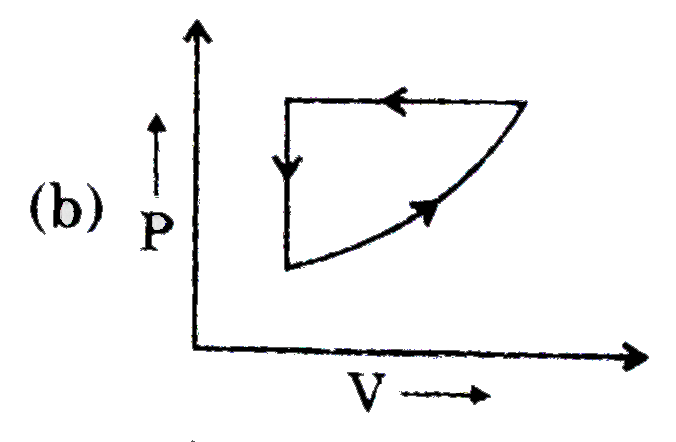 C
C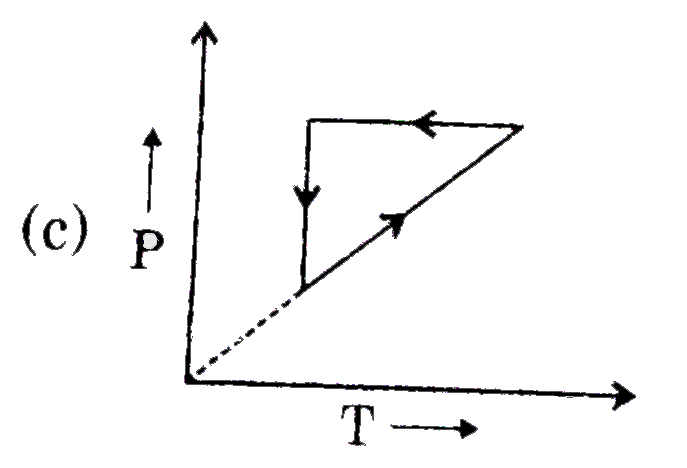 D
D
Three moles of a monoatomic gas is subjected to a rise of temperature 400K under isobaric process. If ratio of increase in internal energy and work done by gas is x10 then find x...
A10B15C25D28
One mole of an ideal monoatomic gas is taken at a temperature of 300K. Its volume is doubled keeping its pressure constant. Find the change in internal energy.
View SolutionFor one mole of an ideal monoatomic gas, volume and temperature are related as V=KT23. If change in temperature of gas is 90K, then work done is given by W = xR. Find value of x
View SolutionOne mole of monoatomic gas undergoes a process as shown in the P-T diagram below. Choose the corresponding V – T diagram.
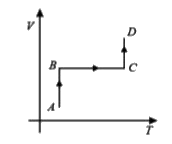
View SolutionExpress the average kinetic energy per mole of a monoatomic gas of molar mass M, at temperature T K in terms of the average speed of the molecules Uavg :
View SolutionWhen 1mol of a monoatomic ideal gas at TK undergoes adiabatic change under a constant external pressure of 1atm, changes volume from 1L→2L. The final temperature (in K) would be
View Solution