![Given I to II isobaric II to III ischoric III to I isothermal Calculate | work done | in cyclic process (in atm xx lit) [nearest Integer]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/JM_23_M2_20230124_CHE_22_Q01.png)
Given
I→II isobaric
II→III ischoric
III→I isothermal
Calculate | work done | in cyclic process (in atm × lit) [nearest Integer]
The correct Answer is:12
Topper's Solved these Questions
Similar Questions
Knowledge Check
StatementI: A gas is expanded from a volume V to 2V, first through adiabatic process then through isothermal process. Work done in isothermal process is more if final state (i.e. pressure and volume ) in both the cases is same

Statement II: Work done by the gas is equal to area under p−V curve.AStatement I: is true, Statement II is true and Statement II is the correct explanation for Statement I.BStatement I: is true, Statement II is true and Statement II is NOT the correct explanation for Statement I.CStatement I is true, Statement II is false.DStatement I is false, Statement II is true.The internal energy of a system remains constant when it undergoes
(i) a cyclic process
(ii) an isothermal process
(iii) an adiabatic process
(iv) any process in which the heat given out by the system equal to the work done on the systemA(i),(iii)B(ii)C(ii),(iv)D(i),(ii),(iv)
One mole of ideal gas undergoes following cyclic process
(i) Isochoric heating from (P1V1T1) to double temperature.
(II) Isobaric expansion from to double voulme .
(III) Linear expansion ( on PV curve) to (P1,8V1).
Isobaric copmression to initial state.
Calculate the magnitude of work done in calories if initial tremperature of the gas in is 300K?
Given : R=2Calmol−K

View SolutionOne mol an ideal gas is expanded from(10atm,10lit). (2atm,50lit) isothermally . First against 5 atm
then against 2 atm . Calculate work done in each step and compare it with single step work done.
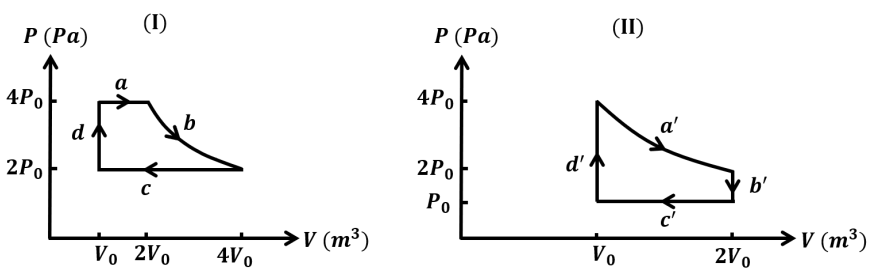
View SolutionOne mole of an ideal gas undergoes two different cyclic processes I and II, as shown in the P - V diagrams belowIn cycle I, processes a, b, c and d are isobaric, isothermal, isobaric and isochoric, respectively. In cycle IIprocesses a' b' , cand d' are isothermal, isochoric, isobaric and isochoric, respectivelyThe total work done during cycle I is WI and that during cycle II is WII. The ratio WI /WII is
View SolutionThe internal energy of a system remains constant when it undergoes
(i) a cyclic process
(ii) an isothermal process
(iii) an adiabatic process
(iv) any process in which the heat given out by the system equal to the work done on the system
View SolutionOne mole of an ideal gas undergoes a cyclic change ABCD. Calculate from the diagram. (P is in atm, and V in litre)
(i) Work done along AB, BC, CD and DA.
(ii) What is the net work done in the process ?
(iii). What is the efficiency of the process ?
(iv) What is the net change in internal energy of the gas ?
Given 1atm=1.01×105Nm−2
View SolutionOne mole of mono-atomic ideal gas is taken along two cyclic processes and as shown in the PV diagram. The processes involved are purely isobaric, isothermal or adiabatic.
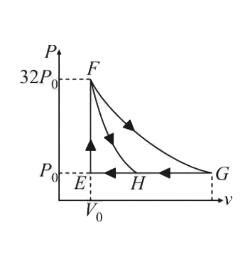
Match the paths in Column I with the magnitudes of the work done in column II and select the correct answer using the codes given below the lists.

View Solution


