One mole of ideal gas undergoes following cyclic process
(i) Isochoric heating from (P1V1T1) to double temperature.
(II) Isobaric expansion from to double voulme .
(III) Linear expansion ( on PV curve) to (P1,8V1).
Isobaric copmression to initial state.
Calculate the magnitude of work done in calories if initial tremperature of the gas in is 300K?
Given : R=2Calmol−K

Magniude of work = A=P1V1+12×P1×6V1
=4×1×2×300
=4×1×2×300
=2400cal
Topper's Solved these Questions
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Exercise
14 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Exercise 1
35 Videos
- THERMODYNAMICSBOOK - BANSALCHAPTER - THERMODYNAMICSEXERCISE - Exercise 3
43 Videos
- THERMOCHEMISTRYBOOK - BANSALCHAPTER - THERMOCHEMISTRYEXERCISE - Exercise 4
15 Videos
Similar Questions
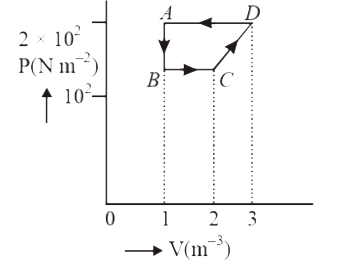
The P-V diagram of a gas system undergoing cyclic process is shown here. The work done during isobaric compression is
View SolutionTwo moles of an ideal gas undergo the following process :
(a) a reversible isobaric expansion from (P atm, VL) to (P atm , 2VL).
(b) a reversible isochoric change of state from (P atm , 2V,L) to (P/2 atm, 2VL)
(c) a reversible isothermal compression from (P/2 atm, 2VL) to (P atm, VL).
Sketch with labels each of the processes on the same P−V diagram.
View Solution
Knowledge Check
An ideal gas follows a process described by PV2=C from (P1,V1,T1) to (P2,V2,T2) (C is a constant). Then
Aif P1>P2 then T2>T1Bif V2>V1 then T2<T1Cif V2>V1 then T2>T1Dif P1>P2 then V1>V2Two moles of an ideal gas undergo the following process :
(a) a reversible isobaric expansion from (P atm, VL) to (P atm , 2VL).
(b) a reversible isochoric change of state from (P atm , 2V,L) to (P/2 atm, 2VL)
(c) a reversible isothermal compression from (P/2 atm, 2VL) to (P atm, VL).
Sketch with labels each of the processes on the same P−V diagram.A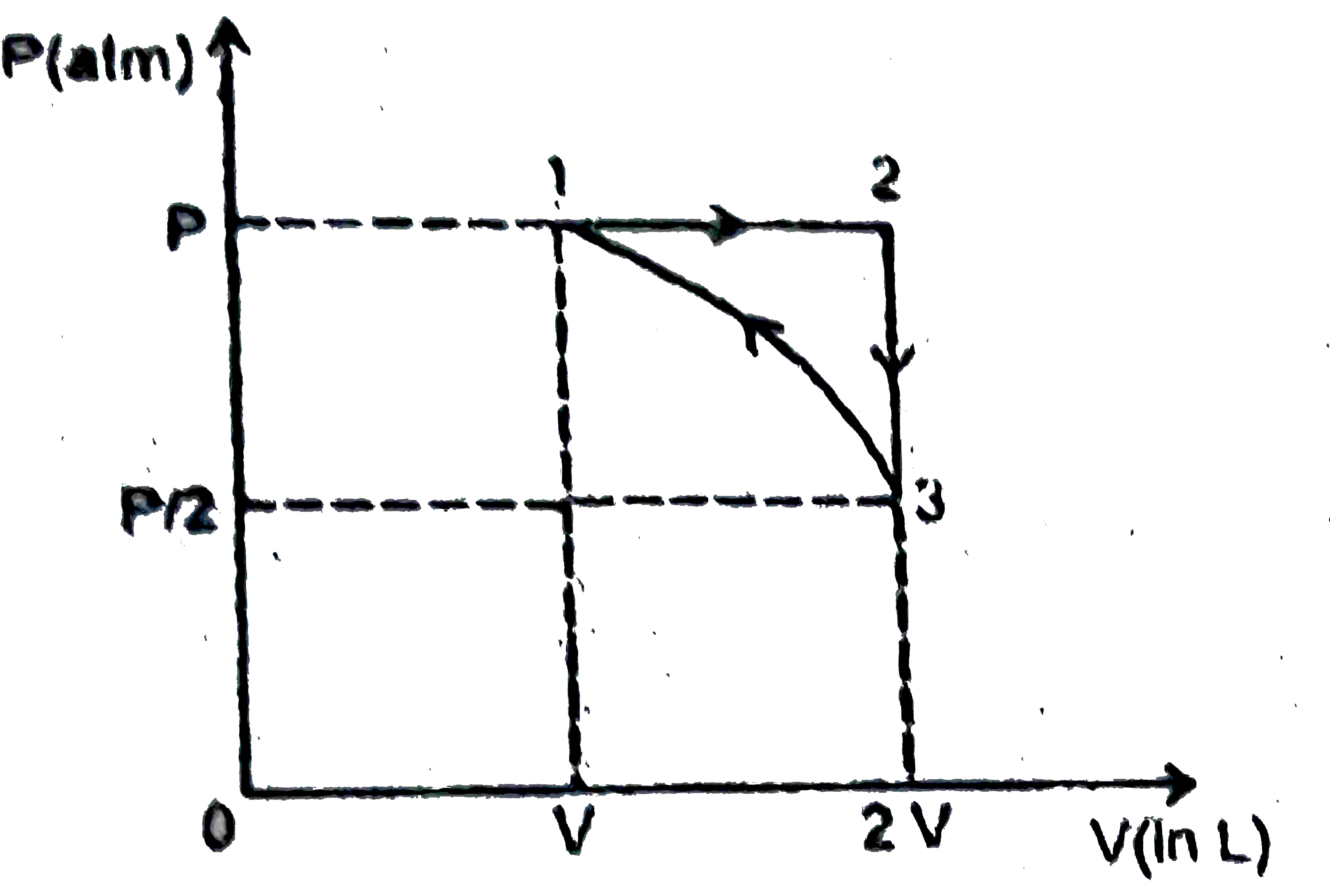 B
B C
C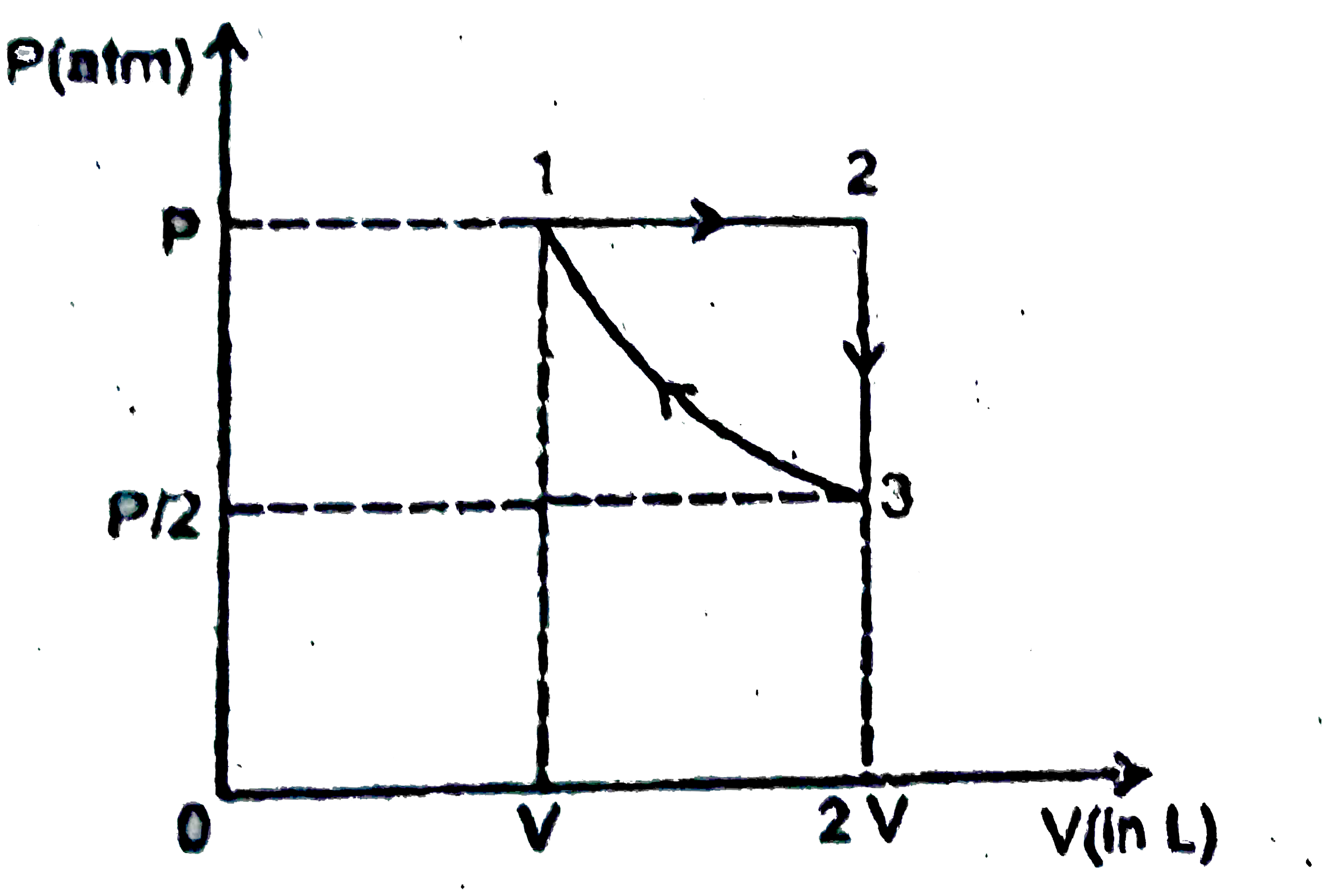 D
D
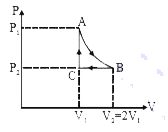
n mole a perfect gas undergoes a cyclic process ABCA (see figure) consisting of the following processes.
A→B: Isothermal expansion at temperature T so that the volume is doubled from V1 to V2=2V1 and pressure changes from P1 to P2
B→C : Isobaric compression at pressure P2 to initial volume V1
C→A : Isochoric change leading to change of pressure from P2 toP1 .
Total work done in the complete cycle ABCA is :
 A0BnRT(ln2+12)CnRTln2DnRT(ln2−12)
A0BnRT(ln2+12)CnRTln2DnRT(ln2−12)
Write expression for the work done by 1 mole of the gas in each of the following cases :
(i) For irreversible expansion of the gas from volume V1 to V2.
(ii) For reversible isothermal expansion of the gas from volume V1 toV2.
(iii)For expansion of the gas into an evaluated vessel.
(iv) For reversible isothermal compression of the gas from pressure P1 to P2
(v)For adiabatic expansion resulting into change of temperature from T1 to T2.
View SolutionCalculate the work of an isobaric reversible expansion of three moles of an ideal gas while it is heated from 298 K to 400 K.
View SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionOne mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionOne mole of a gas in the state A(P1,V1,T1) is subjected to adiabatic expansion to attain state B(P2,V2,T2). The work done by the gas is:
View Solution
