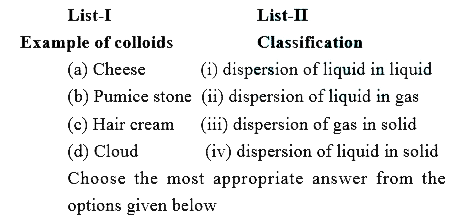Given below are two statements :
Statement I : Stopping potential in photoelectric effect does not depend on the power of the light source.
Statement II : For a given metal,the maximum kinetic energy of the photoelectron depends on the wavelength of the incident light.
In the light of above statements,choose the most appropriate answers from the options given below
Both Statement I and are incorrect
Statement I is correct but statement II are incorrect
Both Statement I and statement II are correct
Statement I is incorrect but statement II is correct
The correct Answer is:C
To solve the question, we need to analyze both statements regarding the photoelectric effect.
Step 1: Analyze Statement I
- Statement I claims that the stopping potential in the photoelectric effect does not depend on the power of the light source.
- The stopping potential (V₀) is determined by the maximum kinetic energy of the emitted photoelectrons, which is given by the equation:
K.Emax=eV0=hν−ϕ
where h is Planck's constant, ν is the frequency of the incident light, and ϕ is the work function of the metal.
- The stopping potential is independent of the intensity (or power) of the light source; it only depends on the frequency (or wavelength) of the incident light.
- Therefore, Statement I is true.
Step 2: Analyze Statement II
- Statement II states that for a given metal, the maximum kinetic energy of the photoelectron depends on the wavelength of the incident light.
- The maximum kinetic energy of the emitted photoelectrons can also be expressed in terms of wavelength (λ) as:
K.Emax=hcλ−ϕ
where c is the speed of light.
- This equation shows that the maximum kinetic energy of the photoelectrons is inversely related to the wavelength of the incident light. Hence, as the wavelength decreases (or frequency increases), the maximum kinetic energy increases.
- Therefore, Statement II is also true.
Step 3: Conclusion
- Both statements are true. Thus, the correct answer is that both Statement I and Statement II are correct.
Final Answer:
Both statements are true.
---
- Statement I claims that the stopping potential in the photoelectric effect does not depend on the power of the light source.
- The stopping potential (V₀) is determined by the maximum kinetic energy of the emitted photoelectrons, which is given by the equation:
K.Emax=eV0=hν−ϕ
where h is Planck's constant, ν is the frequency of the incident light, and ϕ is the work function of the metal.
- The stopping potential is independent of the intensity (or power) of the light source; it only depends on the frequency (or wavelength) of the incident light.
- Therefore, Statement I is true.
- Statement II states that for a given metal, the maximum kinetic energy of the photoelectron depends on the wavelength of the incident light.
- The maximum kinetic energy of the emitted photoelectrons can also be expressed in terms of wavelength (λ) as:
K.Emax=hcλ−ϕ
where c is the speed of light.
- This equation shows that the maximum kinetic energy of the photoelectrons is inversely related to the wavelength of the incident light. Hence, as the wavelength decreases (or frequency increases), the maximum kinetic energy increases.
- Therefore, Statement II is also true.
- Both statements are true. Thus, the correct answer is that both Statement I and Statement II are correct.
Both statements are true.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Match List - I with List- II

Choose the most appropriate answer from the options given below -A(a)→(ii),(b)→(iii),(c)→(iv),(d)→(i)B(a)→(i),(b)→(iv),(c)→(iii),(d)→(ii)C(a)→(i),(b)→(iii),(c)→(iv),(d)→(ii)D(a)→(iv),(b)→(i),(c)→(ii),(d)→(iii)Match List - I with List- II

Choose the most appropriate answer from the options given below -A(a)→(i),(b)→(iii),(c)→(iv),(d)→(ii)B(a)→(ii),(b)→(i),(c)→(iv),(d)→(iii)C(a)→(ii),(b)→(iv),(c)→(i),(d)→(iii)D(a)→(iii),(b)→(i),(c)→(ii),(d)→(iv)
Match List-I with List -II

Choose the most appropriate answer from the options given below:
View SolutionMatch List - I with List - II.

Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List - II.
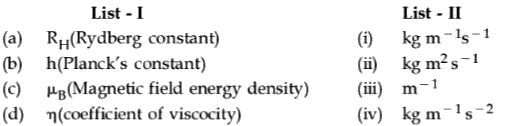
Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List - II
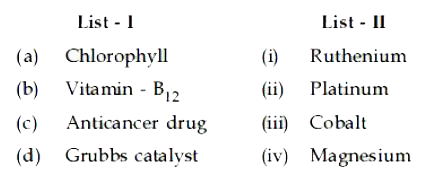
Choose the most appropriate answer from the options given below :
View SolutionMatch List - I with List - II.

Choose the most appropriate answer from the options given below :
View SolutionMatch List -I with List -II :
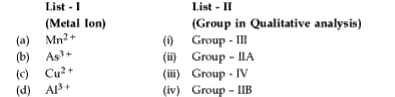
Choose the most appropriate answer from the options given below :
View Solution