A capacitor has capacitance 5μF when it's parallel plates are separated by air medium of thickness d.A slab of material of dielectric constant 1.5 having area equal to that of plates but thickness d2 is inserted between the plates.Capacitance of the capacitor in the presence of slab will be_____μF
To solve the problem, we need to determine the capacitance of a capacitor when a dielectric slab is inserted between its plates. Here’s a step-by-step solution:
Step 1: Understand the Initial Capacitance
The initial capacitance C0 of the capacitor with air as the dielectric is given as:
C0=5μF
Step 2: Identify the Parameters
- The thickness of the air gap (initial separation) is d.
- The dielectric slab has a dielectric constant k=1.5 and thickness d2.
- The area of the plates A remains the same.
Step 3: Capacitance with Dielectric Slab
When the dielectric slab is inserted, we can think of the capacitor as two capacitors in series:
1. The first capacitor C1 is the part with the dielectric slab.
2. The second capacitor C2 is the part with air.
- The thickness of the dielectric slab is d2, and the remaining air gap is also d2.
Step 4: Calculate Individual Capacitances
The capacitance of a parallel plate capacitor is given by:
C=ϵAd
where ϵ=ϵ0k for a dielectric and ϵ0 is the permittivity of free space.
1. For the dielectric slab C1:
C1=ϵ0⋅1.5⋅Ad2=3ϵ0Ad
2. For the air gap C2:
C2=ϵ0⋅Ad2=2ϵ0Ad
Step 5: Combine the Capacitances in Series
The total capacitance C for capacitors in series is given by:
1C=1C1+1C2
Substituting the values of C1 and C2:
1C=13ϵ0Ad+12ϵ0Ad=d3ϵ0A+d2ϵ0A
Step 6: Finding a Common Denominator
To combine the fractions:
1C=2d6ϵ0A+3d6ϵ0A=5d6ϵ0A
Step 7: Solve for Total Capacitance
Taking the reciprocal gives:
C=6ϵ0A5d
Step 8: Relate to Initial Capacitance
We know that:
C0=ϵ0Ad⟹ϵ0A=C0d
Substituting this into the equation for C:
C=6⋅C0d5d=65C0
Step 9: Calculate the Final Capacitance
Substituting C0=5μF:
C=65⋅5μF=6μF
Final Answer
The capacitance of the capacitor in the presence of the slab will be:
6μF
The initial capacitance C0 of the capacitor with air as the dielectric is given as:
C0=5μF
- The thickness of the air gap (initial separation) is d.
- The dielectric slab has a dielectric constant k=1.5 and thickness d2.
- The area of the plates A remains the same.
When the dielectric slab is inserted, we can think of the capacitor as two capacitors in series:
1. The first capacitor C1 is the part with the dielectric slab.
2. The second capacitor C2 is the part with air.
The capacitance of a parallel plate capacitor is given by:
C=ϵAd
where ϵ=ϵ0k for a dielectric and ϵ0 is the permittivity of free space.
C1=ϵ0⋅1.5⋅Ad2=3ϵ0Ad
C2=ϵ0⋅Ad2=2ϵ0Ad
The total capacitance C for capacitors in series is given by:
1C=1C1+1C2
1C=13ϵ0Ad+12ϵ0Ad=d3ϵ0A+d2ϵ0A
To combine the fractions:
1C=2d6ϵ0A+3d6ϵ0A=5d6ϵ0A
Taking the reciprocal gives:
C=6ϵ0A5d
We know that:
C0=ϵ0Ad⟹ϵ0A=C0d
C=6⋅C0d5d=65C0
Substituting C0=5μF:
C=65⋅5μF=6μF
The capacitance of the capacitor in the presence of the slab will be:
6μF
Topper's Solved these Questions
Similar Questions
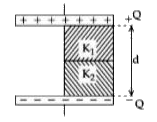
A parallel-plate capacitor with plate area A has separation d between the plates. Two dielectric slabs of dielectric constant K1 and K2 of same area A/2 and thickness d/2 are inserted in the space between the plates. The capacitance of the capacitor will be given by :
 View Solution
View SolutionA parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will the capacitancee of the capacitor. ? Justify your answer
View Solution
Knowledge Check
- Question 1 - Select One
Separation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
Aε0Ad+t(1−1k)Bε0Ad+t(1+1k)Cε0Ad−t(1−1k)Dε0Ad−t(1+1k) - Question 2 - Select One
A parallel -plate air capacitor has capacity C. A dielectric slab of dielectric constant K, whose thickness is half of the air gap between the plates, is now inserted between the plates. The capacity of the capacitor will now be
AKC/2B2KC/(K+1)C2KC/(K−1)DC(K+1)/(K−1) - Question 3 - Select One
A parallel plate condenser has initially air medium between the plates. If a slab of dielectric constant 5 having thickness half the distance of separation between the plates is introduced, the percentage increase in its capacity is.
A33.3%B66.7%C0.5D0.75
A slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the platesView SolutionA slab of material of dielectric constant K has the same area as the plates of a parallel capacitor, but has a thickness (34d),
where d is the separation of the plates. How is the capacitance changed when the slab is inserted between the platesView SolutionA slab of material of dielectric constant k has the same area as that of the plates of a parallel plate capacitor but has the thickness d/2, when d is the separation between the plates. Find out the expression for its capacitance when the slab is inserted between the plates of the capacitor.
View SolutionA parallel plate capacitor has a capacitance of 60 PF, when the plates of the capacitor and separated by a distance d. if a metal plate of thickness t=d3 is introduced between the plates, the capacitance will be
View SolutionA parallel state air capacitor has capacitance of 100 μF. The plates are at a distance d apart. If a slab of thickness t (t≤d) and dielectric constant 5 is introduced between the parallel plates, then the capacitance can be
View Solution

