In an experiment for estimating the value of focal length of converging mirror,image of an object placed at 40cm from the pole of the mirror is formed at distance 120cm from the pole of the mirror.These distances are measured with a modified scale in which there are 20 small divisions in 1cm.The value of error in measurement of focal length of the mirror is 1Kcm.The value of K is
The correct Answer is:B, C
To solve the problem, we need to find the value of K in the context of the error in the measurement of the focal length of a converging mirror.
1. Understand the Given Information:
- The object distance u=−40cm (negative as per the sign convention).
- The image distance v=−120cm (also negative).
- The distances are measured with a scale that has 20 small divisions in 1 cm, which gives us the least count Δu=Δv=120cm.
2. Use the Mirror Formula:
The mirror formula is given by:
1f=1v+1u
Substituting the values of u and v:
1f=1−120+1−40
3. Calculate 1f:
1f=−1120−140
To combine these fractions, find a common denominator (which is 120):
1f=−1120−3120=−4120=−130
Thus, f=−30cm.
4. Calculate the Error in Focal Length:
The formula for the error in focal length is given by:
Δff2=Δvv2+Δuu2
Since Δu=Δv=120, we can substitute:
Δf(−30)2=120(−120)2+120(−40)2
5. Calculate Each Term:
- For v=−120:
Δv(−120)2=12014400=1288000
- For u=−40:
Δu(−40)2=1201600=132000
6. Combine the Errors:
Δf900=1288000+132000
Finding a common denominator (which is 288000):
132000=9288000
Thus,
Δf900=1+9288000=10288000
7. Solve for Δf:
Δf=10×900288000=9000288000=132cm
8. Relate to K:
The problem states that the error in measurement of focal length is given as 1Kcm. Therefore, we have:
1K=132⟹K=32
Final Answer:
Thus, the value of K is 32.
- The object distance u=−40cm (negative as per the sign convention).
- The image distance v=−120cm (also negative).
- The distances are measured with a scale that has 20 small divisions in 1 cm, which gives us the least count Δu=Δv=120cm.
The mirror formula is given by:
1f=1v+1u
Substituting the values of u and v:
1f=1−120+1−40
1f=−1120−140
To combine these fractions, find a common denominator (which is 120):
1f=−1120−3120=−4120=−130
Thus, f=−30cm.
The formula for the error in focal length is given by:
Δff2=Δvv2+Δuu2
Since Δu=Δv=120, we can substitute:
Δf(−30)2=120(−120)2+120(−40)2
- For v=−120:
Δv(−120)2=12014400=1288000
- For u=−40:
Δu(−40)2=1201600=132000
Δf900=1288000+132000
Finding a common denominator (which is 288000):
132000=9288000
Thus,
Δf900=1+9288000=10288000
Δf=10×900288000=9000288000=132cm
The problem states that the error in measurement of focal length is given as 1Kcm. Therefore, we have:
1K=132⟹K=32
Thus, the value of K is 32.
Topper's Solved these Questions
Similar Questions
An object is placed at 20 cm from the pole of a concave mirror. It forms real image at a distance of 60 cm from the pole. Find the focal length of the concave mirror.
View SolutionThe image of an object placed 16 cm from a concave mirror is formed at a distance of 24 cm from the mirror. Calculate the possible focal lengths of the concave mirror from this information.
View Solution
Knowledge Check
- Question 1 - Select One
An object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
AinfinityB10 cmC15 cmD40 cm - Question 2 - Select One
In an experiment to find the focal lengh of a concave mirror, an object is palced at a distance of 40 cm from it and forms image at 24 cm from the mirror, ten the focal length is
A−15 cmB−16 cmC−30 cmD−32 cm - Question 3 - Select One
An object is placed 10 cm in front of a convex mirror of focal length 20 cm . The distance of the image from the mirror is
A10/3 cmB20/3 cmC10 cmD40/3 cm
An object is placed 40 cm from the concave mirror with a focal length of 20 cm . The image formed is :
View SolutionA concave mirror has focal length 15cm. If an object is placed at a distance of 30 cm from the mirror, then image formed by the mirror lies at a distance (from the mirror)
View SolutionA convex mirror of focal length 10cm is shown in figure. A linear object AB=5cm is placed along the optical axis. Point B is at distance 25cm from the pole of mirror. The size of image of AB is
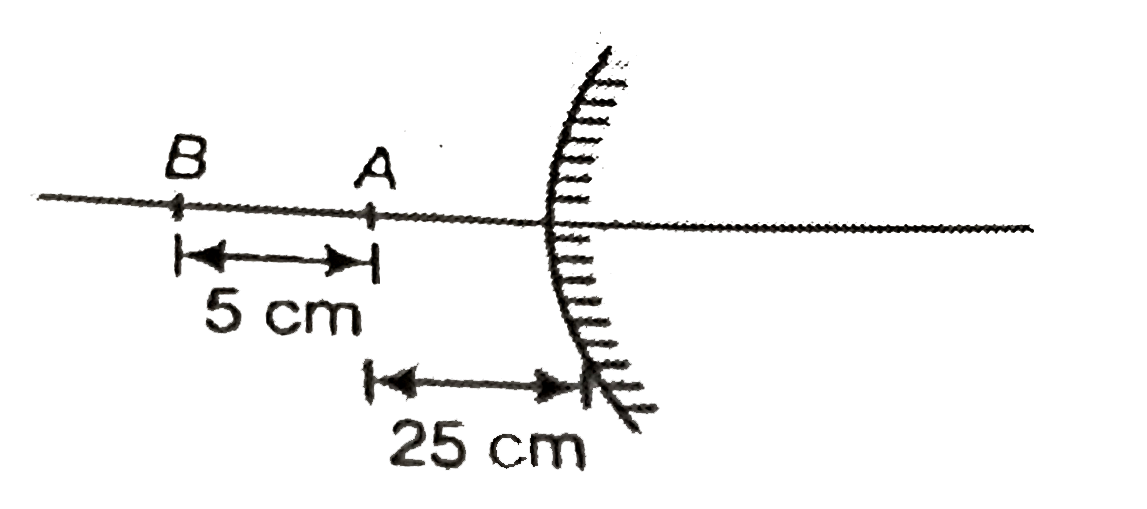 View Solution
View SolutionA real object is placed at a distance f from the pole of a convex mirror, infront of the convex mirror. If focal length of the mirror is f, then distance of the image from the pole of the mirror is
View SolutionA point object is placed on the axis of the concave mirror at a distance of 60 cm from the focal point of the mirror. Its image is formed at the point of object then focal length of the mirror is
View Solution

