A body of mass 2kg is initially at rest.It starts moving unidirectionally under the influence of a source of constant power P.Its displacement in 4s is 13α2√Pm.The value of α will be
To solve the problem, we need to find the value of α given the displacement of a body under constant power. Let's break it down step by step.
Step 1: Understand the relationship between power, work, and displacement
The power P is defined as the rate of doing work, which can be expressed as:
P=dWdt
where dW is the work done. The work done on the body is equal to the change in kinetic energy, which can be expressed as:
dW=F⋅dx
where F is the force applied and dx is the displacement.
Step 2: Relate power to displacement
For a body of mass m moving under a constant power, we can derive the relationship between displacement x and time t:
x=23√2Pmt3/2
Step 3: Substitute the known values
Given:
- Mass m=2kg
- Time t=4s
Substituting these values into the displacement equation:
x=23√2P2(4)3/2
This simplifies to:
x=23√P(4)3/2
Step 4: Calculate (4)3/2
Calculating (4)3/2:
(4)3/2=(22)3/2=23=8
So, we can rewrite the displacement as:
x=23√P⋅8=163√P
Step 5: Set the displacement equal to the given expression
We are given that the displacement in 4 seconds is:
x=13α2√Pm
Substituting m=2:
x=13α2√2P
Step 6: Equate the two expressions for displacement
Now we equate the two expressions for x:
163√P=13α2√2P
Step 7: Simplify the equation
Multiplying both sides by 3:
16√P=α2√2P
Dividing both sides by √P (assuming P≠0):
16=α2√2
Step 8: Solve for α
Now, squaring both sides:
162=α4⋅2
256=2α4
Dividing both sides by 2:
α4=128
Taking the fourth root:
α=√(4)128=√(4)64⋅2=√8=2√2
Conclusion
Thus, the value of α is:
α=4
The power P is defined as the rate of doing work, which can be expressed as:
P=dWdt
where dW is the work done. The work done on the body is equal to the change in kinetic energy, which can be expressed as:
dW=F⋅dx
where F is the force applied and dx is the displacement.
For a body of mass m moving under a constant power, we can derive the relationship between displacement x and time t:
x=23√2Pmt3/2
Given:
- Mass m=2kg
- Time t=4s
x=23√2P2(4)3/2
This simplifies to:
x=23√P(4)3/2
Calculating (4)3/2:
(4)3/2=(22)3/2=23=8
So, we can rewrite the displacement as:
x=23√P⋅8=163√P
We are given that the displacement in 4 seconds is:
x=13α2√Pm
Substituting m=2:
x=13α2√2P
Now we equate the two expressions for x:
163√P=13α2√2P
Multiplying both sides by 3:
16√P=α2√2P
Dividing both sides by √P (assuming P≠0):
16=α2√2
Now, squaring both sides:
162=α4⋅2
256=2α4
Dividing both sides by 2:
α4=128
Taking the fourth root:
α=√(4)128=√(4)64⋅2=√8=2√2
Thus, the value of α is:
α=4
Topper's Solved these Questions
Similar Questions
A body is moving undirectionally under the influence of a source of constatn power. It displacement in time t is proportional to (i) t1/2 (ii) t (iii) t3/2 (iv) t2
View SolutionA body undergoing a straight line motion is under the influence of source of constant power. How does its displacement very with time?
View Solution
Knowledge Check
A body is moving unidirectionally under the influence of a sources of constant power. The square of its displacement in time t is proportional to
At3Bt2CtD√tA body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
A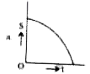 B
B C
C D
D
A body is moving unidirectionally under the influence of a source of constant power supplying energy. Which of the diagrams shown in figure. Correctly shows the displacement-time curve for its motion ?
A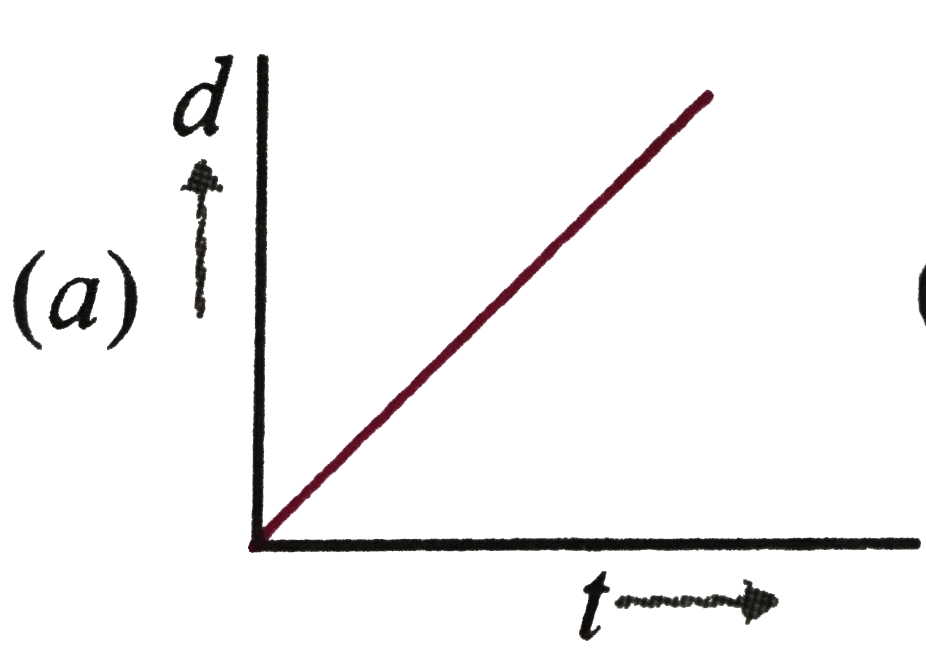 B
B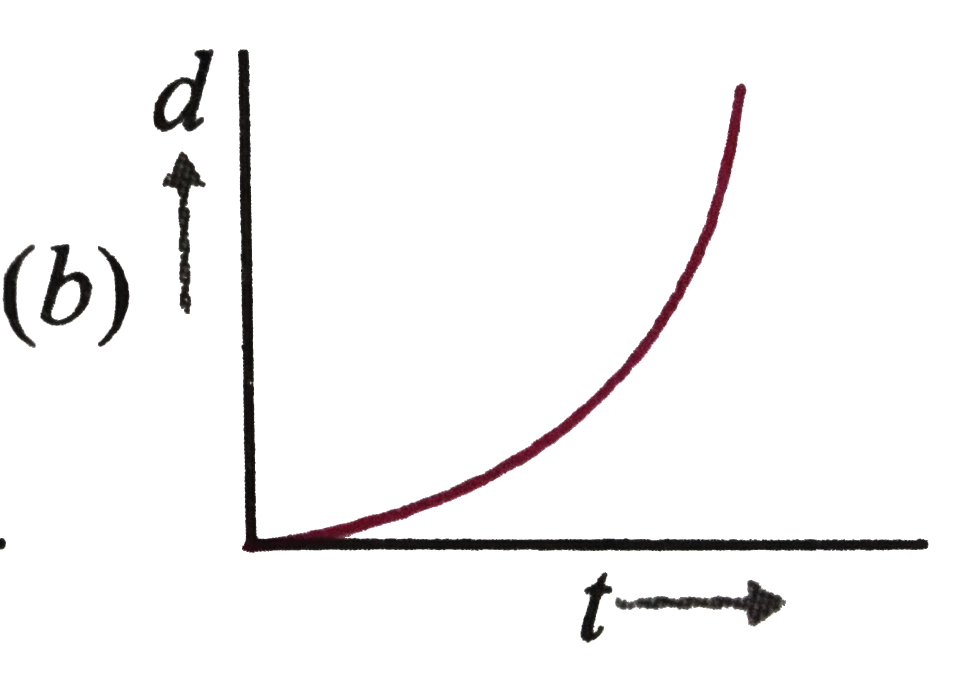 C
C D
D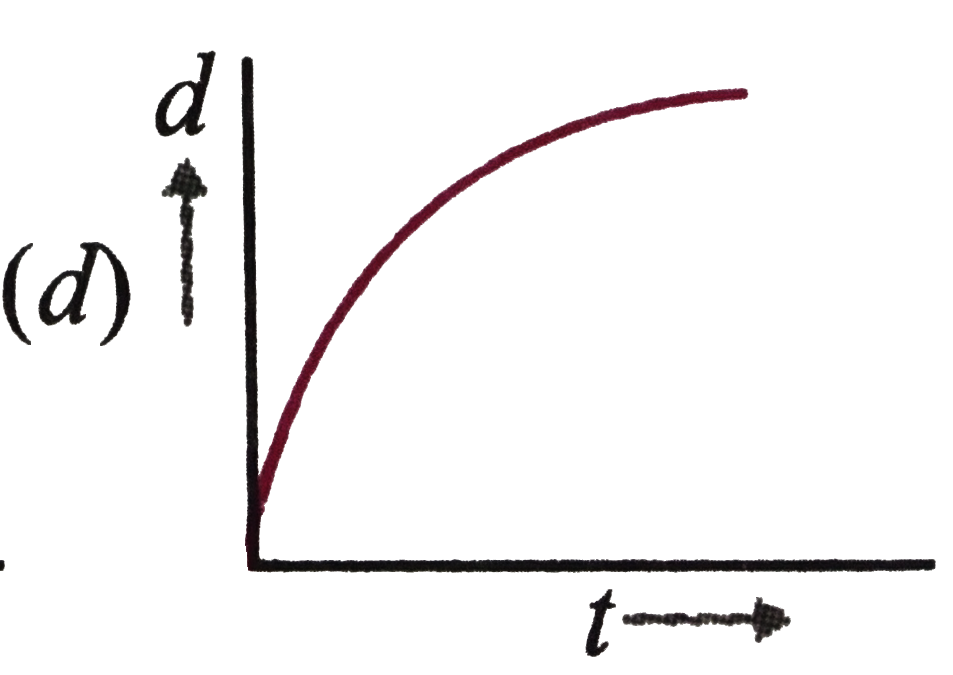
A body of mass 2 kg is at rest. What should be the magnitude of force which will make the body move with a speed of 30 m/s at the end of 1 s?
View SolutionA particle of mass 0.2kg is moving in one dimension under a force that delivers constant power 0.5W to the particle. If the initial speed (in ms−1) after 5s is.
View SolutionA body of mass 2kg at rest is supplied constant power 1J/sec, the distance travelled by body after 6 sec is
View SolutionA body lying initially at point (3,7) starts moving with a constant acceleration of 4ˆi. Its position after 3s is given by the coordinates
View SolutionA body of mass 2kg starts from rest and moves with uniform acceleration. It acquires a velocity 20ms−1 in 4s.
The power exerted on the body at 2s is
View Solution
