A body of mass 2kg at rest is supplied constant power 1J/sec, the distance travelled by body after 6 sec is
2√6 m
4√m
2 sqrt3 m
6 sqrt3 m
The correct Answer is:B
To solve the problem of finding the distance traveled by a body of mass 2 kg under constant power of 1 J/s after 6 seconds, we can follow these steps:
1. Understanding the Given Information:
- Mass of the body, m=2kg
- Initial velocity, u=0m/s (the body is at rest)
- Power supplied, P=1J/s
- Time, t=6s
2. Using the Work-Energy Theorem:
The work done on the body is equal to the change in kinetic energy:
W=ΔK
The work done can also be expressed in terms of power:
W=P⋅t
Therefore, we can write:
P⋅t=ΔK
3. Calculating Work Done:
Substitute the values of power and time:
W=1J/s⋅6s=6J
4. Finding the Change in Kinetic Energy:
The change in kinetic energy is given by:
ΔK=12mv2−12mu2
Since the initial velocity u=0:
ΔK=12mv2
Setting this equal to the work done:
6=12⋅2⋅v2
Simplifying gives:
6=v2
Therefore:
v=√6m/s
5. Finding the Distance Traveled:
The distance traveled under constant acceleration can be found using the formula:
s=ut+12at2
Since the body starts from rest, u=0. We need to find the acceleration a:
P=F⋅v⟹F=Pv=1√6N
Using Newton's second law:
F=m⋅a⟹a=Fm=1/√62=12√6m/s2
6. Calculating the Distance:
Now substituting a into the distance formula:
s=0+12(12√6)(62)=12⋅12√6⋅36
Simplifying gives:
s=18√6=3√6m
Final Result:
The distance traveled by the body after 6 seconds is:
s=3√6meters
- Mass of the body, m=2kg
- Initial velocity, u=0m/s (the body is at rest)
- Power supplied, P=1J/s
- Time, t=6s
The work done on the body is equal to the change in kinetic energy:
W=ΔK
The work done can also be expressed in terms of power:
W=P⋅t
Therefore, we can write:
P⋅t=ΔK
Substitute the values of power and time:
W=1J/s⋅6s=6J
The change in kinetic energy is given by:
ΔK=12mv2−12mu2
Since the initial velocity u=0:
ΔK=12mv2
Setting this equal to the work done:
6=12⋅2⋅v2
Simplifying gives:
6=v2
Therefore:
v=√6m/s
The distance traveled under constant acceleration can be found using the formula:
s=ut+12at2
Since the body starts from rest, u=0. We need to find the acceleration a:
P=F⋅v⟹F=Pv=1√6N
Using Newton's second law:
F=m⋅a⟹a=Fm=1/√62=12√6m/s2
Now substituting a into the distance formula:
s=0+12(12√6)(62)=12⋅12√6⋅36
Simplifying gives:
s=18√6=3√6m
The distance traveled by the body after 6 seconds is:
s=3√6meters
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given v-t graph, the distance travelled by the body in 5 sec will be :
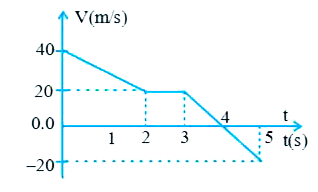 A100 mB80 mC40 mD20 m
A100 mB80 mC40 mD20 mA body at rest is moved in a stright line by supplying constant power to it . Distance moved by the body in time t is found to be proportional to tn Value of n is .
A3/2B2/3C12D3/4The velocity versus time graph of a body moving in a straight line is as follows. The distance travelled by the body is 5 sec is
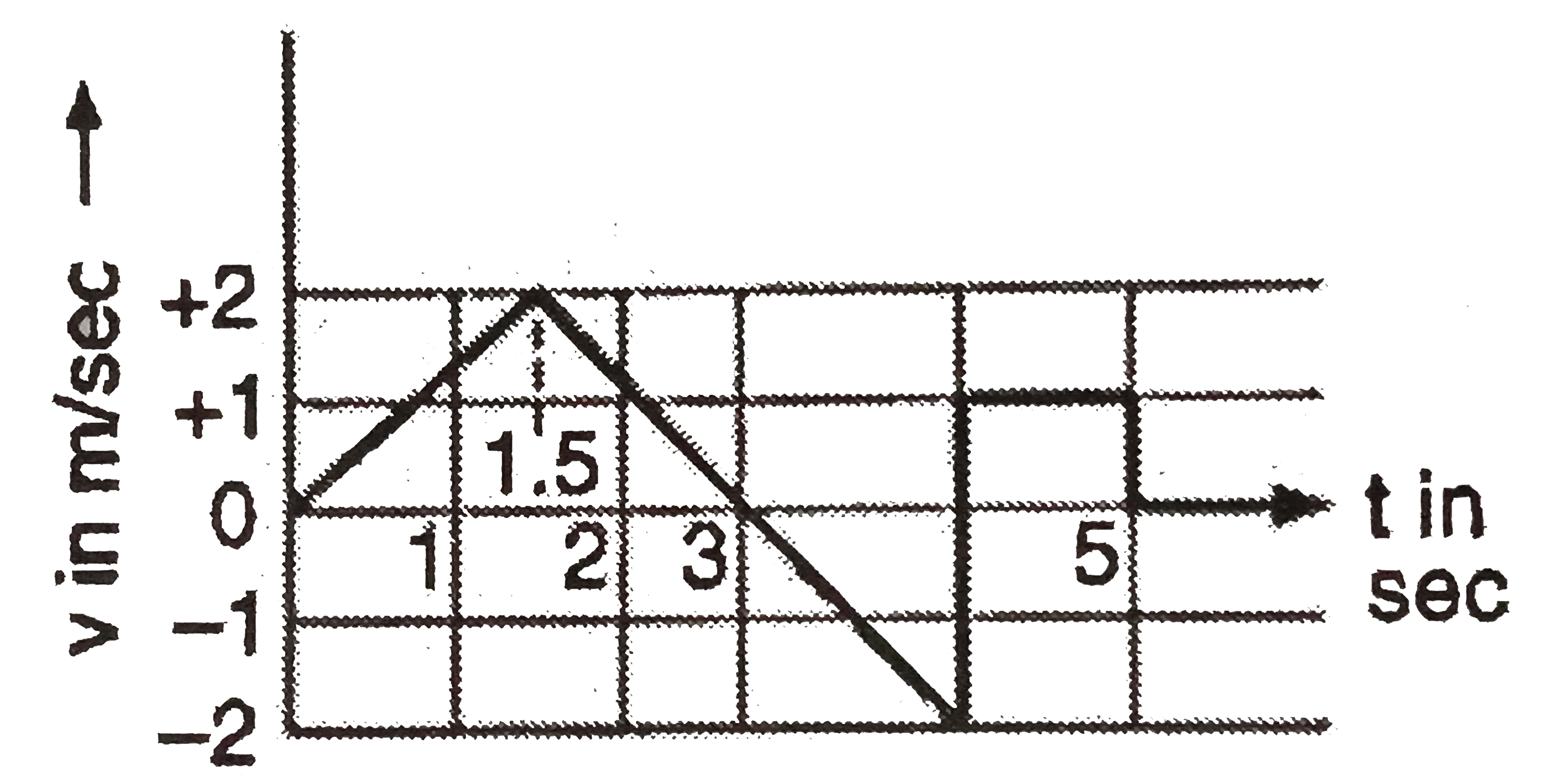 A2 mB3 mC4 mD5 m
A2 mB3 mC4 mD5 m
A body of mass 2 kg is driven by an engine delivering a constant power of 1 J /s. The body starts from rest and moves in a straight line. After 9 seconds, the body has moved a distance ( in m) ……….. .
View SolutionA body of mass 3 kg travelling with a velocity 5m/s collides head - on and elastically with a body of mass 2kg travelling at a speed 5m/s in opposite direction.The velocity of the second body after the collision is?
View SolutionA body starting from rest and has uniform acceleration
8m/s2 . The distance travelled by it in5th second will be
View SolutionA body of mass 4 kg is accelerated up by a constant force, travels a distance of 5 m in the first second and a distance of 2m in the third second. The force acting on the body is
View SolutionA body of mass 3 kg at rest is acted upon by a force and the body moves through a distance 20 m in 5 s. Force on the body is
View Solution
