For hydrogen atom, $λ_{1}$ and $λ_{2}$ are the wavelengths corresponding to the transitions $x 1$ and $2$ respectively as shown in figure.The ratio of $λ_{1}$ and $λ_{2}$ is $\frac{x}{32}$ .The value of $x$ is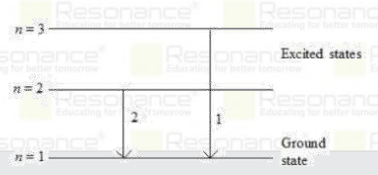

Video Solution

Answer

Step by step video & image solution for For hydrogen atom, lambda_(1) and lambda_(2) are the wavelengths corresponding to the transitions x1 and 2 respectively as shown in figure.The ratio of lambda_(1) and lambda_(2) is (x)/(32).The value of x is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS JEE MAINS 2023 JAN ACTUAL PAPER

Topper's Solved these Questions

JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS (SECTION -B)
10 Videos

Knowledge Check

If $λ_{1}$ and $λ_{2}$ are the wavelength of characteristic $X$ - rays and gamma rays respectively , then the relation between them is
A $λ_{1} = \frac{1}{λ_{2}}$
B $λ_{1} = λ_{2}$
C $λ_{1} > λ_{2}$
D $λ_{1} < λ_{2}$
if $λ_{v'}, λ_{x}$ and $λ_{m}$ represent the wavelengths of visible light X-rays and microwaves respectively then:
A $λ_{m} > λ_{x} > λ_{v}$
B $λ_{k} > λ_{m} > λ_{x}$
C $λ_{m} > λ_{v} > λ_{x}$
D $λ_{y} > λ_{x} > λ_{m}$
If $λ_{1} and λ_{2}$ , are the wavelengths of the third member of Lyman and first member of the Paschen series respectively, then the value of $λ_{1} : λ_{2}$ is:
A $1 : 9$
B $7 : 108$
C $7 : 135$
D $1 : 3$

JEE MAINS PREVIOUS YEAR-JEE MAINS 2023 JAN ACTUAL PAPER-Question

Home
Ask Doubt
Profile

For hydrogen atom, λ1 and λ2 are the wavelengths corresponding to the transitions x1 and 2 respectively as shown in figure.The ratio of λ1 and λ2 is x32.The value of x is

Topper's Solved these Questions

Similar Questions

Knowledge Check

If λ1 and λ2 are the wavelength of characteristic X - rays and gamma rays respectively , then the relation between them is

if λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:

If λ1andλ2 , are the wavelengths of the third member of Lyman and first member of the Paschen series respectively, then the value of λ1:λ2 is:

JEE MAINS PREVIOUS YEAR-JEE MAINS 2023 JAN ACTUAL PAPER-Question

For hydrogen atom, $λ_{1}$ and $λ_{2}$ are the wavelengths corresponding to the transitions $x 1$ and $2$ respectively as shown in figure.The ratio of $λ_{1}$ and $λ_{2}$ is $\frac{x}{32}$ .The value of $x$ is

If $λ_{1}$ and $λ_{2}$ are the wavelength of characteristic $X$ - rays and gamma rays respectively , then the relation between them is

if $λ_{v'}, λ_{x}$ and $λ_{m}$ represent the wavelengths of visible light X-rays and microwaves respectively then:

If $λ_{1} and λ_{2}$ , are the wavelengths of the third member of Lyman and first member of the Paschen series respectively, then the value of $λ_{1} : λ_{2}$ is: