The speed of a swimmer is in still water.If the swimmer makes his strokes normal to the flow of river of width ,he reaches a point down the stream on the opposite bank. The speed of the river water is _____
To solve the problem, we need to analyze the swimmer's movement across the river and how the river's current affects his path. Let's break down the solution step by step.
Step 1: Understand the Problem
The swimmer has a speed of 4 km/h in still water and swims perpendicular to the current of the river. The river has a width of 1 km (1000 m), and the swimmer ends up 750 m downstream on the opposite bank. We need to find the speed of the river (Vr).
Step 2: Set Up the Geometry
When the swimmer swims straight across the river, he is affected by the current of the river. The swimmer's path can be visualized as a right triangle:
- The width of the river (1 km or 1000 m) is one side (perpendicular).
- The distance he is carried downstream (750 m) is the other side (base).
- The swimmer's effective path forms the hypotenuse.
Step 3: Calculate the Angle
Using the tangent function, we can find the angle (θ) of the swimmer's path:
tan(θ)=oppositeadjacent=750 m1000 m=0.75
This means:
θ=tan−1(0.75)
Step 4: Relate the Speeds
The swimmer's speed in still water (Vs) is 4 km/h. The speed of the river (Vr) will affect how far downstream he is carried. The effective horizontal speed of the swimmer can be expressed as:
Vr=Vs⋅tan(θ)
Substituting the value of tan(θ):
Vr=4 km/h⋅34=3 km/h
Step 5: Conclusion
The speed of the river (Vr) is 3 km/h.
Final Answer
The speed of the river water is 3 km/h.
---
The swimmer has a speed of 4 km/h in still water and swims perpendicular to the current of the river. The river has a width of 1 km (1000 m), and the swimmer ends up 750 m downstream on the opposite bank. We need to find the speed of the river (Vr).
When the swimmer swims straight across the river, he is affected by the current of the river. The swimmer's path can be visualized as a right triangle:
- The width of the river (1 km or 1000 m) is one side (perpendicular).
- The distance he is carried downstream (750 m) is the other side (base).
- The swimmer's effective path forms the hypotenuse.
Using the tangent function, we can find the angle (θ) of the swimmer's path:
tan(θ)=oppositeadjacent=750 m1000 m=0.75
This means:
θ=tan−1(0.75)
The swimmer's speed in still water (Vs) is 4 km/h. The speed of the river (Vr) will affect how far downstream he is carried. The effective horizontal speed of the swimmer can be expressed as:
Vr=Vs⋅tan(θ)
Substituting the value of tan(θ):
Vr=4 km/h⋅34=3 km/h
The speed of the river (Vr) is 3 km/h.
The speed of the river water is 3 km/h.
Topper's Solved these Questions
Similar Questions
A man can swim at a speed 2ms−1 in still water. He starts swimming in a river at an angle 150∘ with direction of flow of water and reaches at the exactly oppsite point on the opposite bank.
(a) Find the speed of flowing water.
(b) If width of river is 1 km then calculate the time taken also
View SolutionThe speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View Solution
Knowledge Check
The river flows at 4 km/h. A boat can go downstream thrice as fast as upstream The speed of boat in still water is
A12 km/hB16 km/hC8 km/hD10 km/hThe speed of boat is 5kmh−1 in still water. It crosses a river of width 1 km along the shortest possible path in 15 min. Then, velocity of river will be
A4.5kmh−1B4kmh−1C.5kmh−1D3kmh−1A boat which has a speed of 6km/h in still water crosses a river of width 1 km along the shortest possible path in 20 min. the velocity of the river water in km/h is
A1B3C4D3√3
A boat man can rown with a speed of 10kmh−1 in still water. If the river flows steadily at 5km/h, in which direction showld the boatman row in order to reach a point on the other bank directly opposite to the point from wher he stared ? The width of the river is 2km.
View SolutionIf the speed of a swimmer in still water is 9 km/h. Find the down stream speed of the swimmer,whenthe river is flowing with the speed of 6 km/h.
View SolutionA man can swim with a speed of 4kmh−1 in still water. He crosses a river 1km wise that flows steadily at 3kmh−1. If he makes his strokes normal to the river current, how far down the river does he go when he reaches the other bank?
View SolutionA boat crosses a river of width 1 km by shortest path in 15 min. if the speed of boat in still water is 5 kmh−1, then what is the speed of the river?
View SolutionA swimmer wands to cross a river and reach point B directly from A. The speed of the wimmer in still river and that of river flow are same. The dotted line AN is normal to flow direction of river. For swimmer to reach point B, the angle his velocity relative to river will make with line AN is given by θ. then the value of θ is :
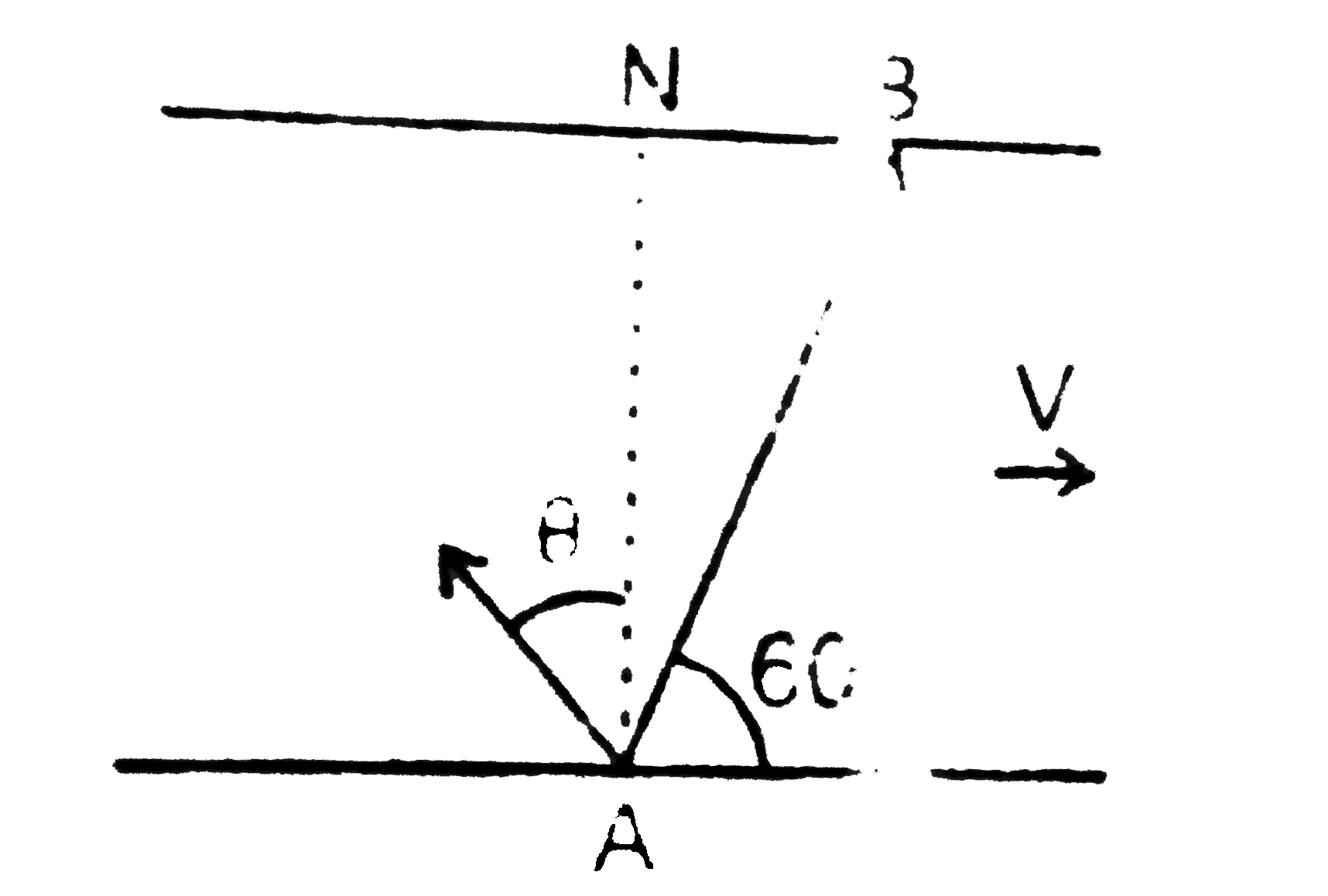
View Solution
