For a charged spherical ball,electrostatic potential inside the ball varies with r as V=2ar2+b.Here,a and b are constant and r is the distance from the centre.The volume charge density inside the ball is −λaɛ.The value of λ is _____ɛ= permittivity of the medium
To solve the problem, we need to find the value of λ given the electrostatic potential V inside a charged spherical ball and the volume charge density.
1. Given Information:
- The electrostatic potential inside the ball is given by:
V=2ar2+b
- The volume charge density is given as:
ρ=−λaε
2. Finding the Electric Field:
- The electric field E can be derived from the potential V using the relation:
E=−dVdr
- Differentiate V with respect to r:
dVdr=ddr(2ar2+b)=4ar
- Therefore, the electric field E becomes:
E=−dVdr=−4ar
3. Using Gauss's Law:
- According to Gauss's law, the electric field E at a distance r from the center of a sphere with charge density ρ is given by:
E⋅4πr2=Qencε0
- The charge enclosed Qenc can be expressed in terms of the volume charge density ρ:
Qenc=ρ⋅Volume=ρ⋅43πr3
- Substituting ρ=−λaε:
Qenc=−λaε⋅43πr3
4. Substituting into Gauss's Law:
- Substitute E and Qenc into Gauss's law:
(−4ar)⋅4πr2=−λaε⋅43πr3ε0
- Simplifying the left side:
−16πar3=−λaε⋅43πr3ε0
5. Canceling Common Terms:
- Cancel πr3 from both sides (assuming r≠0):
−16a=−λaεε0⋅43
- Rearranging gives:
16=λεε0⋅43
6. Solving for λ:
- Multiply both sides by 34:
λ=16⋅34⋅ε0ε=12⋅ε0ε
- Since we are looking for the value of λ in terms of constants, we can take ε0=ε in a normalized medium, thus:
λ=12
Final Answer:
λ=12
- The electrostatic potential inside the ball is given by:
V=2ar2+b
- The volume charge density is given as:
ρ=−λaε
- The electric field E can be derived from the potential V using the relation:
E=−dVdr
- Differentiate V with respect to r:
dVdr=ddr(2ar2+b)=4ar
- Therefore, the electric field E becomes:
E=−dVdr=−4ar
- According to Gauss's law, the electric field E at a distance r from the center of a sphere with charge density ρ is given by:
E⋅4πr2=Qencε0
- The charge enclosed Qenc can be expressed in terms of the volume charge density ρ:
Qenc=ρ⋅Volume=ρ⋅43πr3
- Substituting ρ=−λaε:
Qenc=−λaε⋅43πr3
- Substitute E and Qenc into Gauss's law:
(−4ar)⋅4πr2=−λaε⋅43πr3ε0
- Simplifying the left side:
−16πar3=−λaε⋅43πr3ε0
- Cancel πr3 from both sides (assuming r≠0):
−16a=−λaεε0⋅43
- Rearranging gives:
16=λεε0⋅43
- Multiply both sides by 34:
λ=16⋅34⋅ε0ε=12⋅ε0ε
- Since we are looking for the value of λ in terms of constants, we can take ε0=ε in a normalized medium, thus:
λ=12
λ=12
Topper's Solved these Questions
Similar Questions
The electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b, where r is distance from the center of the ball, a and b are constants. Calculate the charge density inside the ball.
View SolutionA solid sphere of radius R is charged with volume charge density p=Krn , where K and n are constants and r is the distance from its centre. If electric field inside the sphere at distance r is proportional to r4 ,then find the value of n.
View Solution
Knowledge Check
The electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
A(a) −6aε0rB(b) −24πaε0C(c) −6aε0D(d) −24πaε0rThe electrostatic potential inside a charged spherical ball is given by ϕ=ar2+b where r is the distance from the centre and a, b are constants. Then the charge density inside the ball is:
A−24πaε0rB−6πε0rC−24πaε0D−6aε0The dependence of electric potential V on the distance 'r' from the centre of a charged spherical shell is shown by :
A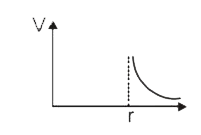 B
B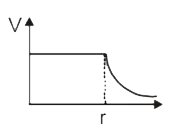 C
C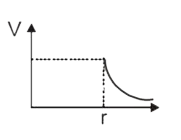 D
D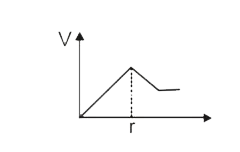
The electric potential in a region is given as V=−4ar2+3b, where r is distance from the origin, a and b are constants. If the volume charge density in the region is given by ρ=naε0, then what is the value of n?
View SolutionInside a hollow charged spherical conductor the potential Is constant Varies directly as the distance from the centre Varies inversely as the distance from the centre Varies inversely as the square of the distance from the centre
View SolutionThe potential inside a charged ball depends only on the distance r of the point form its centre according to the following relation V=Ar2+Bvo<s The charge density inside the ball will be
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionPotential at a point x-distance from the centre inside the conducting sphere of radius R and charged with charge Q is
View Solution
