Unpolarised light is incident on the boundary between two dielectric media whose dielectric constants are (medium-1) and (medium-2),respectively.To satisfy the condition,so that the reflected by refracted rays are perpendicular to each other,the angle of incidence should be the value of is_______ (Given for dielectric media,
To solve the problem, we need to find the value of θ given the dielectric constants of two media and the condition that the reflected and refracted rays are perpendicular to each other.
1. Identify the Dielectric Constants:
- Let k1=2.8 (for medium-1)
- Let k2=6.8 (for medium-2)
2. Use the Condition for Perpendicular Rays:
- The condition for the reflected and refracted rays to be perpendicular is given by:
tan(ϕ)=√k2k1
- Here, ϕ is the angle of refraction.
3. Substitute the Values of Dielectric Constants:
- Substitute the values of k1 and k2:
tan(ϕ)=√6.82.8
4. Calculate the Ratio:
- Calculate 6.82.8:
6.82.8=6828=177
- Therefore,
tan(ϕ)=√177
5. Relate to the Given Condition:
- According to the problem, we have:
tan(ϕ)=√1+10θ
6. Set the Two Expressions Equal:
- Set the two expressions for tan(ϕ) equal to each other:
√177=√1+10θ
7. Square Both Sides:
- Squaring both sides gives:
177=1+10θ
8. Rearranging the Equation:
- Rearranging gives:
10θ=177−1
- Simplifying the right-hand side:
177−1=177−77=107
9. Solve for θ:
- Now, we have:
10θ=107
- Cross-multiplying gives:
10⋅7=10⋅θ
- Therefore:
θ=7
Final Answer:
The value of θ is 7.
- Let k1=2.8 (for medium-1)
- Let k2=6.8 (for medium-2)
- The condition for the reflected and refracted rays to be perpendicular is given by:
tan(ϕ)=√k2k1
- Here, ϕ is the angle of refraction.
- Substitute the values of k1 and k2:
tan(ϕ)=√6.82.8
- Calculate 6.82.8:
6.82.8=6828=177
- Therefore,
tan(ϕ)=√177
- According to the problem, we have:
tan(ϕ)=√1+10θ
- Set the two expressions for tan(ϕ) equal to each other:
√177=√1+10θ
- Squaring both sides gives:
177=1+10θ
- Rearranging gives:
10θ=177−1
- Simplifying the right-hand side:
177−1=177−77=107
- Now, we have:
10θ=107
- Cross-multiplying gives:
10⋅7=10⋅θ
- Therefore:
θ=7
The value of θ is 7.
Topper's Solved these Questions
Similar Questions
Find the angle of refraction for a ray of light falling on a transparent medium of refractive index 1.6.
The reflected and refracted rays are perpendicular to each other.
View SolutionA ray of light falls on a transparent slab of μ=1.732. If reflected and refracted rays are mutually perpendicular, what is the angle of incidence ?
View Solution
Knowledge Check
A ray of light falls on a transparent slab of μ=1.0. If reflected and refracted rays are mutually perpendicular, what is the angle of incidence ?
A45∘B60∘C30∘D90∘A ray of light from a denser medium strikes a rarer medium at an angle of incidence i. if the reflected and the refracted rays are mutually perpendicular to each other, what is the value of the critical angle ?
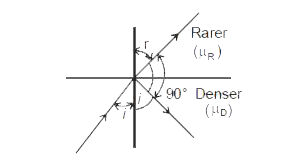 Asin−1(coti)Bcos−1(tani)Csin−1(tani)Dtan−1(sini)
Asin−1(coti)Bcos−1(tani)Csin−1(tani)Dtan−1(sini)The capacitance of a capacitor, filled with two dielectrics of same dimensions but of dielectric constants K1andK2 respectively as shown will be -
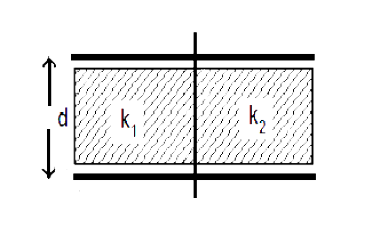 A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A∈0A2d(K1+K2)B∈0Ad(K1+K2)C∈0A2d(K1+K2K1+K2)D∈0Ad(K1K2K1+K2)
A ray of light is incident on a transparent glass slab of refractive index 1.62. If the reflected and refracted rays are mutually perpendicular, what is the angle of incidence ? [tan–1(1.62)=58.3∘]
View SolutionA ray of light is going from rarer to denser medium so that when angle of incidence is 60∘ reflected and refracted rays are perpendicular to each other.The refractive index of denser medium w.r.t.rarer medium is
View SolutionA ray of light from a denser medium strikes a rarer medium at an angle of incidence i=tan−1(1/2). If the reflected and the refracted rays are mutually perpendicular to each-other, what is the value of the critical angle in degree?
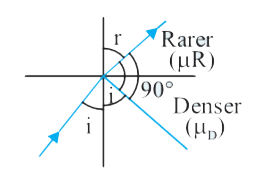
View SolutionLight from a denser medium 1 passes to a rarer medium 2. When the angle of incidence is θ the partially reflected and refracted rays are mutually perpendicular. The critical angle will be

View SolutionA ray of light refracts from medium 1 into a thin layer of medium 2, crosses the layer and is incident at the critical angle on the interface between the medium 2 and 3 as shown in the figure. If the angle of incidence of ray is θ, the values of θ is
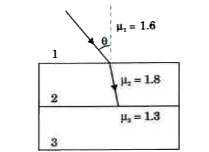
View Solution
