The figure shows v2m versus 1λ raph for photoelectrons emitted from a surface where vm is the maximum speed of electrons and λ is the wavelength of incident radiation. Using this graph and Einstein's photoelectric equation, obtain the expression for Planck's constant andwork function of the surface.
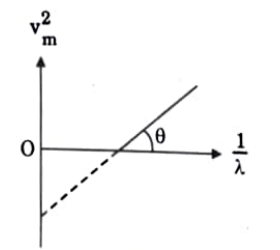
Step by step video solution for The figure shows v_m^2 versus 1/lambda raph for photoelectrons emitted from a surface where v_m is the maximum speed of electrons and lambda is the wavelength of incident radiation. Using this graph and Einstein's photoelectric equation, obtain the expression for Planck's constant andwork function of the surface. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The maximum kinetic energy of photoelectron is doubled when the wavelength of light incident on the photosensitive changes from λ1 to λ2. Deduce expression for the threshold wavelength and work function for metals in terms of λ1 and λ2
View SolutionThe stopping potential for photoelectrons emitted from a surface illuminated by light wavelength of 5893A is 036V. Calculate the maximum kinetic energy of photoelectrons, the work function of the surface, and the threshold frequency.
View Solution
Knowledge Check
The photoelectric work function of a surface is 2.2 eV. The maximum kinetic energy of photoelectrons emitted when light of wavelength 6200 Å is incident on the surface, is
A0.4 eVB1.2 eVC1.6 eVDPhotoelectrons are not emitted.The kinetic energy of the most energetic photoelectrons emitted from a metal surface is doubled when the wavelength of the incident radiation is reduced from λ1 to λ2 The work function of the metal is
Ahcλ1λ2(2λ2−λ1)Bhcλ1λ2(2λ1−λ2)Chcλ1λ2(λ1+λ2)Dhcλ1λ2(λ1−λ2)The maximum velocity of an electron emitted by light of wavelength λ incident on the surface of a metal of work function ϕ, is
Where h = Planck's constant , m = mass of electron and c = speed of light.A[2(hc+λϕ)mλ]1/2B2(hc−λϕ)mC[2(hc−λϕ)mλ]1/2D[2(hλ−ϕ)m]1/2
Maximum kinetic energy of photoelectrons emitted from a metal surface, when light of wavelength λ is incident on it, is 1 eV. When a light of wavelength λ3 is incident on the surfaces, maximum kinetic energy becomes 4 times. The work function of the metal is
View SolutionPhotoelectrons ar ejected from a surface when light of wavelenght λ1=550nm is incident on it. The stopping potential for such electrons is λS1=0.19V. Suppose that radiation of wavelength λ2=190nm is incident of the surface.
Q. Calulate the work function of the surface.
View SolutionThe velocity of the most energetic electrons emitted from a metallic surface is doubled when the frequecy v of incident radiation is double. The work function of this metal is
View SolutionWhen a high frequency electromagnetic radiation is incident on a metallic surface, electrons are emitted from the surface. Energy of emitted photoelectrons depends only on the frequency of incident electromagnetic radiation and the number of emitted electrons depends only on the intensity of incident light.
Einstein's protoelectron equation [Kmax=hv−ϕ} correctly ecplains the PE, where υ= frequency of incident light and ϕ= work function.
Q. The slope of the graph shown if Fig. [here h is the Planck's constant and e is the charge of an electron] is
View SolutionA photon sensitive metallic surface emits electrons when X-rays of wavelength λ fal on it. The de-Broglie wavelength of the emitted electrons is (Neglect the work function of the surface, m is mass of the electron. H=Planck's constant. C= velocity of light)
View Solution
