Two small conducting balls A and B of radius r1 and r2 have charges q1 and q2 respectively. They are connected by a wire.Obtain the expression for charges on A and B, in equilibrium.
To find the expression for the charges on conducting balls A and B in equilibrium, we need to follow these steps:
1. Identify the given parameters:
- Radius of ball A: r1
- Radius of ball B: r2
- Initial charges on ball A: q1
- Initial charges on ball B: q2
2. Understand the equilibrium condition:
When two conducting balls are connected by a wire, they will share charges until they reach the same electric potential. This means the potential V on both balls will be equal.
3. Write the expression for the potential of each ball:
The potential V of a charged sphere is given by:
V=q4πϵ0r
where q is the charge and r is the radius of the sphere.
For ball A:
VA=qA4πϵ0r1
For ball B:
VB=qB4πϵ0r2
4. Set the potentials equal to each other:
Since VA=VB in equilibrium:
qA4πϵ0r1=qB4πϵ0r2
5. Simplify the equation:
qAr1=qBr2
qAr2=qBr1
qAqB=r2r1
6. Express the total charge:
Let Q be the total charge:
Q=qA+qB
7. Solve for qA and qB:
From the ratio qAqB=r2r1, we can write:
qA=r2r1qB
Substitute qA in the total charge equation:
Q=r2r1qB+qB
Q=qB(r2r1+1)
qB=Qr2r1+1
qB=Qr2+r1r1
qB=Qr1r1+r2
Now, substitute qB back into the expression for qA:
qA=r2r1qB
qA=r2r1⋅Qr1r1+r2
qA=Qr2r1+r2
Final Expressions:
- Charge on ball A:
qA=Qr2r1+r2
- Charge on ball B:
qB=Qr1r1+r2
- Radius of ball A: r1
- Radius of ball B: r2
- Initial charges on ball A: q1
- Initial charges on ball B: q2
When two conducting balls are connected by a wire, they will share charges until they reach the same electric potential. This means the potential V on both balls will be equal.
The potential V of a charged sphere is given by:
V=q4πϵ0r
where q is the charge and r is the radius of the sphere.
VA=qA4πϵ0r1
VB=qB4πϵ0r2
Since VA=VB in equilibrium:
qA4πϵ0r1=qB4πϵ0r2
qAr1=qBr2
qAr2=qBr1
qAqB=r2r1
Let Q be the total charge:
Q=qA+qB
From the ratio qAqB=r2r1, we can write:
qA=r2r1qB
Q=r2r1qB+qB
Q=qB(r2r1+1)
qB=Qr2r1+1
qB=Qr2+r1r1
qB=Qr1r1+r2
qA=r2r1qB
qA=r2r1⋅Qr1r1+r2
qA=Qr2r1+r2
- Charge on ball A:
qA=Qr2r1+r2
qB=Qr1r1+r2
Topper's Solved these Questions
Similar Questions
Two concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View SolutionTwo concentric spherical conducting shells of radii R and 2R carry charges Q and 2Qrespectively.Change in electric potential on the outer shell when both are connected by a conducting wire is (k=14πɛ0)
View Solution
Knowledge Check
Two conducting spheres of radii r1 and r2 having charges Q1 and Q2 respectively are connected to each other. There is
Ano change in the energy of the systemBan increase in the energy of the systemCalways a decrease in the energy of the systemDa decrease in the energy of the system unless Q1r2=Q2r1The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
ANo change in the energy of the systemBAn increase in the energy of the systemCAlways a decrease in the energy of the systemDA decrease in the energy of the system unless
Q1R2=Q2R1The insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
ANo change in the electrical energy of the systemBAn increase in the electrical energy of the systemCAlways a decrease in the electrical energy of the systemDA decrease in electrical energy of the system until Q1R2=Q2R3
Two conducting hollow spherical shells of radius R and 2R carry charges -Q and 3Q respectively. How much charge will flow into the earth if inner shell is grounded?
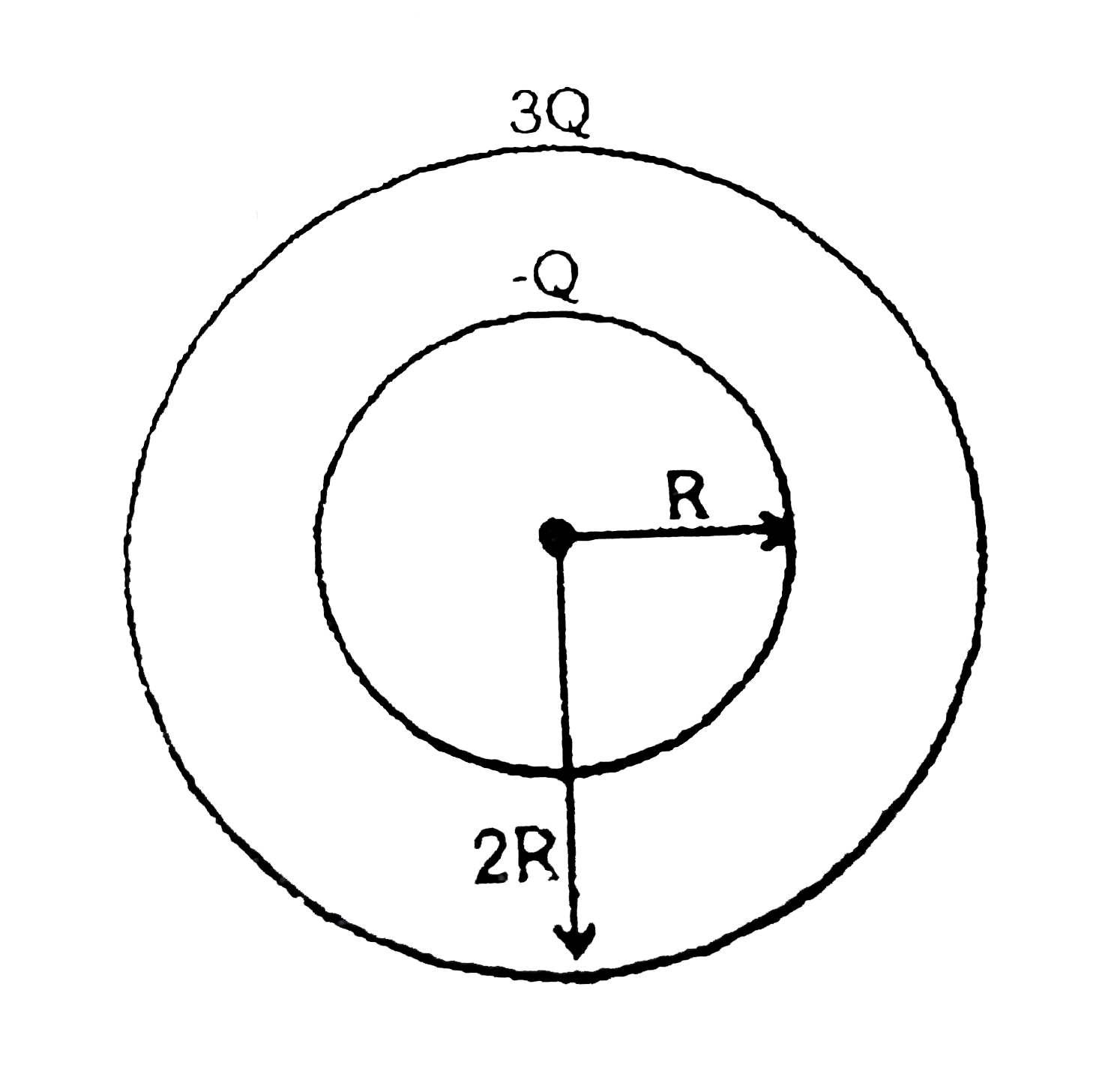
View SolutionTwo concentric spherical conducting shells of radii r and R (r<R) carry charges q and Q respectively . The two shells are now connected by a conducting wire. The final charge on the inner shell is
View SolutionTwo spherical conductors A and B of radii R and 2R respectively are each given a charge Q. When they are connected by a metallic wire. The charge will
View SolutionTwo concentric conducting shells of radius a and b (b>a) carry charges Q and −2Q respectively. The correct variation of electric intensity E as a function of r is given by
View SolutionTwo small conductors A and B are given charges q1andq2 respectively. Now they are placed inside a hollow metallic conductor C carrying a charge Q. If all the three conductors A, B and C are connected by a conducting wire as shown, the charges on A,B and C will be respectively :

View Solution
