The trajectory of projectile, projected from the ground is given by y=x-x^2/20 Where x and y are measured in meter.The maximum height attained by the projectile will be.
5m
200m
10m
10√2 m
To find the maximum height attained by the projectile given the trajectory equation y=x−x220, we will follow these steps:
Step 1: Differentiate the trajectory equation
We start by differentiating the equation with respect to x to find the slope of the trajectory:
dydx=1−2x20=1−x10
Step 2: Set the derivative to zero
To find the maximum height, we set the derivative equal to zero:
1−x10=0
Step 3: Solve for x
Solving the equation gives:
x10=1⟹x=10 meters
Step 4: Substitute x back into the trajectory equation
Now, we substitute x=10 back into the original trajectory equation to find the maximum height y:
y=10−10220
Calculating this:
y=10−10020=10−5=5 meters
Conclusion
The maximum height attained by the projectile is:
5 meters
---
We start by differentiating the equation with respect to x to find the slope of the trajectory:
dydx=1−2x20=1−x10
To find the maximum height, we set the derivative equal to zero:
1−x10=0
Solving the equation gives:
x10=1⟹x=10 meters
Now, we substitute x=10 back into the original trajectory equation to find the maximum height y:
y=10−10220
Calculating this:
y=10−10020=10−5=5 meters
The maximum height attained by the projectile is:
5 meters
Topper's Solved these Questions
Similar Questions
Trajectory of particle in a projectile motion is given as: y=x−(x2/80) (x and y are in meters). Take g=10m/s2.

View SolutionThe equation of path of a particle projected obliquely from the ground under gravity is given by y=2x−x2 where 'x' and ' y' are in meter.The "x" and "y" axes are in horizontal and vertical directions respectively.The speed of projection is
View Solution
Knowledge Check
An object is projected with speed u and range of the projectile is found to be double of the maximum height attained by it . Range of the projectile is .
A2u25gB3u25gC4u25gDu2gAn object is projected with speed u and range of the projectile is found to be double of the maximum height attained by it . Range of the projectile is .
AvA=vB=vCBvA>vB>vCCvA<vB<vCDva=vB>vCThe horizontal range is four times the maximum height attained by a projectile. The angle of projection is
A90∘B60∘C45∘D30∘
Two projectiles are projected from the same point different velocities and different angles of projection .If the maximum height attained by both the projectiles is same, show that sum of the times taken by each to reach the highest point is equal to the total time of flight of either of the projectiles .
View SolutionThe equation of trajectory of a projectile thrown from a point on the ground is y=(x−x240)m. If g=10ms−2 The maximum height reached is
View SolutionTrajectory of particle in a projectile motion is given as y=x−x280. Here, x and y are in meters. For this projectile motion, match the following with g=10m/s2.
Column-IColumn-II(A)Angle of projection (in degrees)(P)20(B)Angle of velocity with horizontal after 4s (in degrees)(Q)80(C)Maximum height (in meters)(R)45(D)Horizontal range (in meters)(S)30(T)60
View SolutionTrajectory of a particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion the following with g=10m/s2.
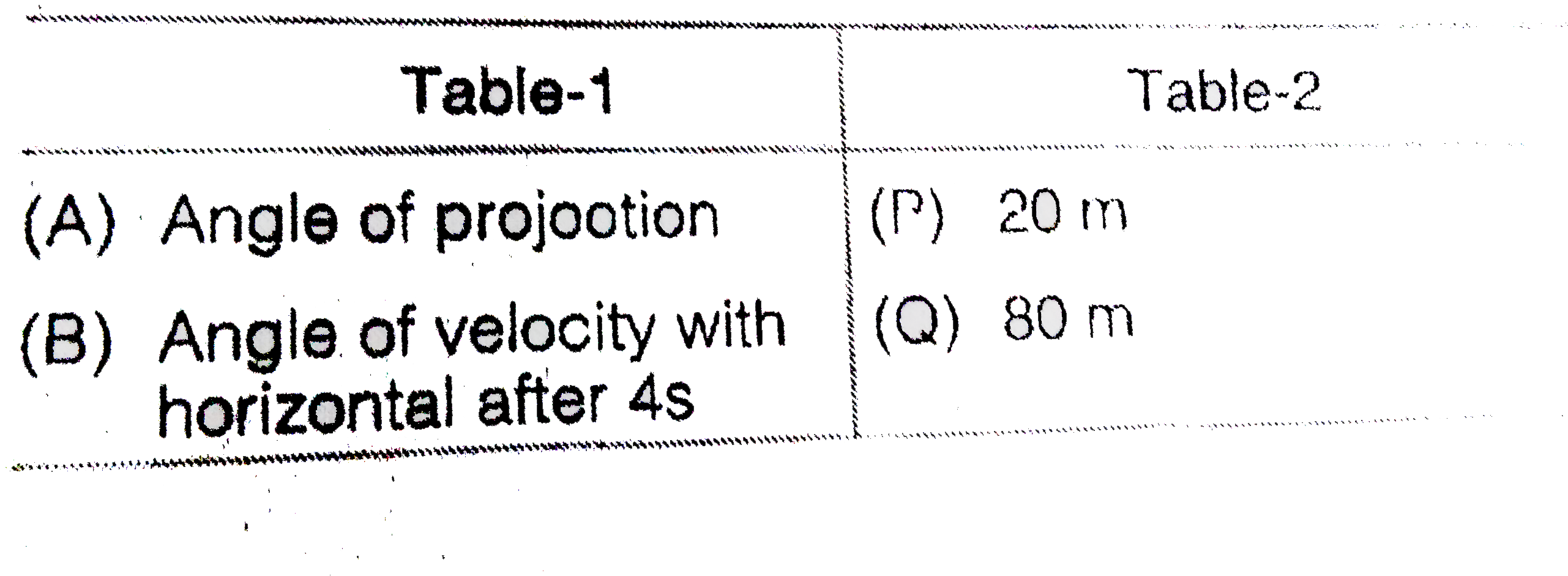
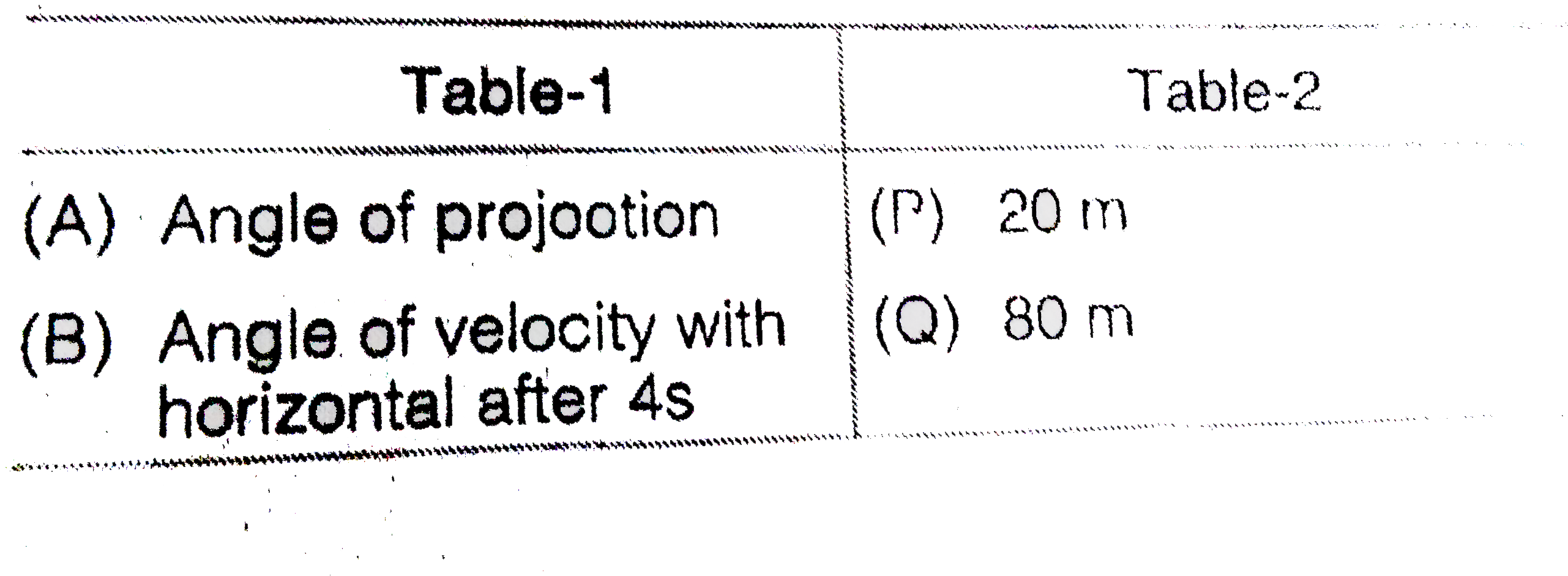
View SolutionTrajectory of particle in projectile motion is y=(x−x2/80), x and y are in metre.
Projectile range is on horizontal plane.

View Solution
