10 resistors each of resistance 10 Ω can be connected in such as to get maximum and minimum equivalent resistanceThe ratio of maximum and minimum equivalent resistance will be
To solve the problem of finding the ratio of maximum and minimum equivalent resistance when connecting 10 resistors each of resistance 10 Ω, we can follow these steps:
Step 1: Determine Maximum Equivalent Resistance
The maximum equivalent resistance occurs when all resistors are connected in series. The formula for the equivalent resistance Req in series is given by:
Req=R1+R2+R3+...+Rn
Since all resistors have the same resistance R=10Ω and there are 10 resistors:
Req=10+10+10+10+10+10+10+10+10+10=10×10=100Ω
Step 2: Determine Minimum Equivalent Resistance
The minimum equivalent resistance occurs when all resistors are connected in parallel. The formula for the equivalent resistance Req in parallel is given by:
1Req=1R1+1R2+1R3+...+1Rn
Again, since all resistors have the same resistance R=10Ω and there are 10 resistors:
1Req=110+110+110+110+110+110+110+110+110+110
1Req=1010=1
Req=1Ω
Step 3: Calculate the Ratio of Maximum to Minimum Resistance
Now that we have both the maximum and minimum equivalent resistances, we can find the ratio:
Ratio=Req(series)Req(parallel)=100Ω1Ω=100
Final Answer
The ratio of maximum to minimum equivalent resistance is:
Ratio=100
---
The maximum equivalent resistance occurs when all resistors are connected in series. The formula for the equivalent resistance Req in series is given by:
The minimum equivalent resistance occurs when all resistors are connected in parallel. The formula for the equivalent resistance Req in parallel is given by:
1Req=1010=1
Req=1Ω
Now that we have both the maximum and minimum equivalent resistances, we can find the ratio:
The ratio of maximum to minimum equivalent resistance is:
Topper's Solved these Questions
Similar Questions
Given n resistors each of resistance R, how will you combine them to get the (i) maximum, and (ii) minimum effective resistance? What is the ratio of the maximum to minimum resistance?
View SolutionThree resistors, each of resistance 12Ω, are connected in parallel. What is the equivalent resistance ?
View Solution
Knowledge Check
- Question 1 - Select One
Eight resistances each of resistance 5Ω are connected in the circuit as shown in figure. The equivalent resistance between A and B is
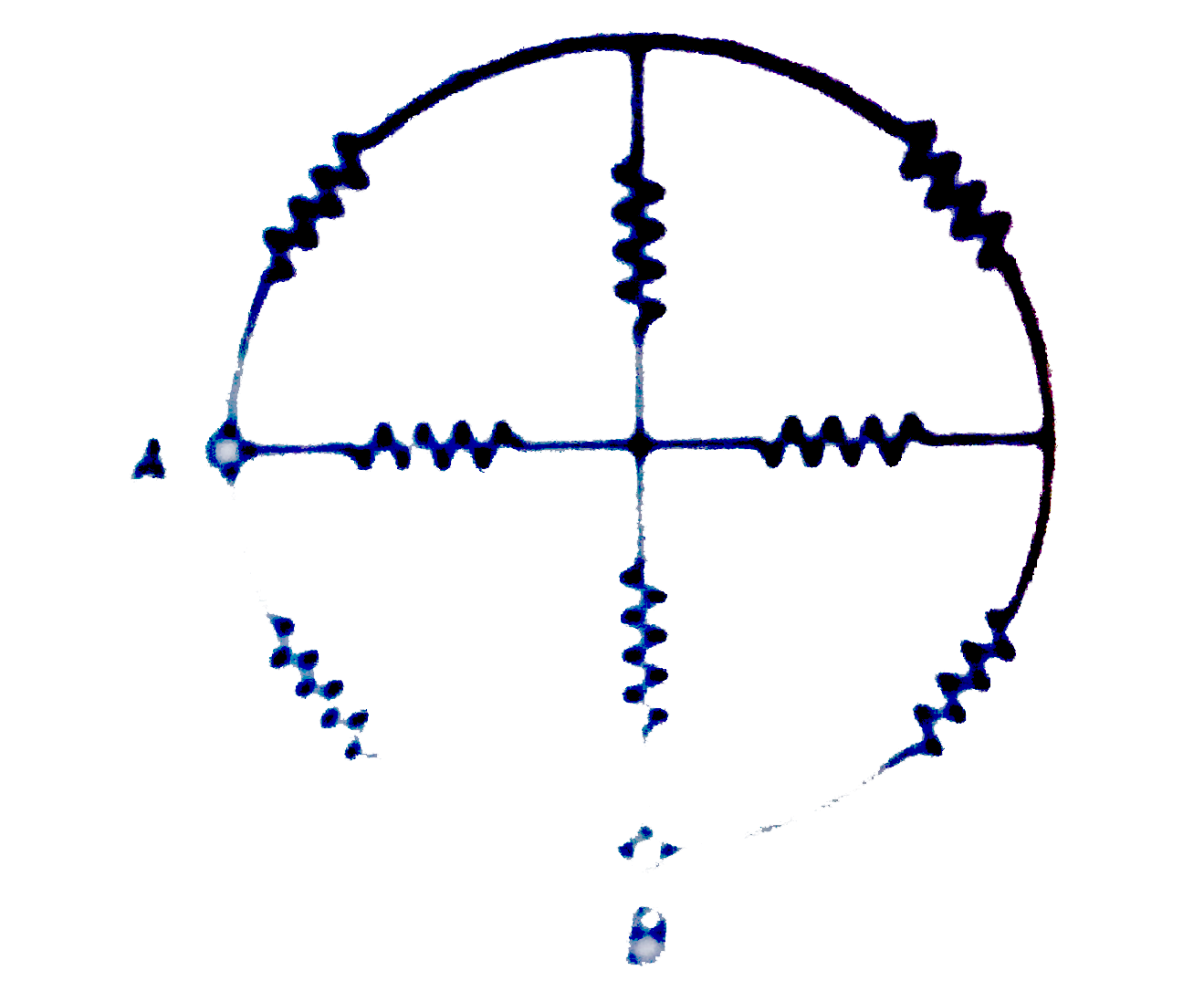 A83ΩB163ΩC157ΩD192Ω
A83ΩB163ΩC157ΩD192Ω - Question 2 - Select One
We have n resistors each of resistance R. The ratio of the combination for maximum and minimum values is
AnBn2Cn3D1n - Question 3 - Select One
The resistors of resistances 2Ω,4Ω and 8Ω are connected in parallel, then the equivalent resistance of the combination will be
A87ΩB78ΩC74ΩD49Ω
(a) Given n resistors each of resistance R. How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of 1Ω,2Ω,3Ω, how will you combine them to get an equivalent resistance of (i) (11/3)Ω (ii) (11/5)Ω (iii) 6Ω (iv) (6/11)Ω ?
(c) Determine the equivalent resistance of networks shown in Figure.
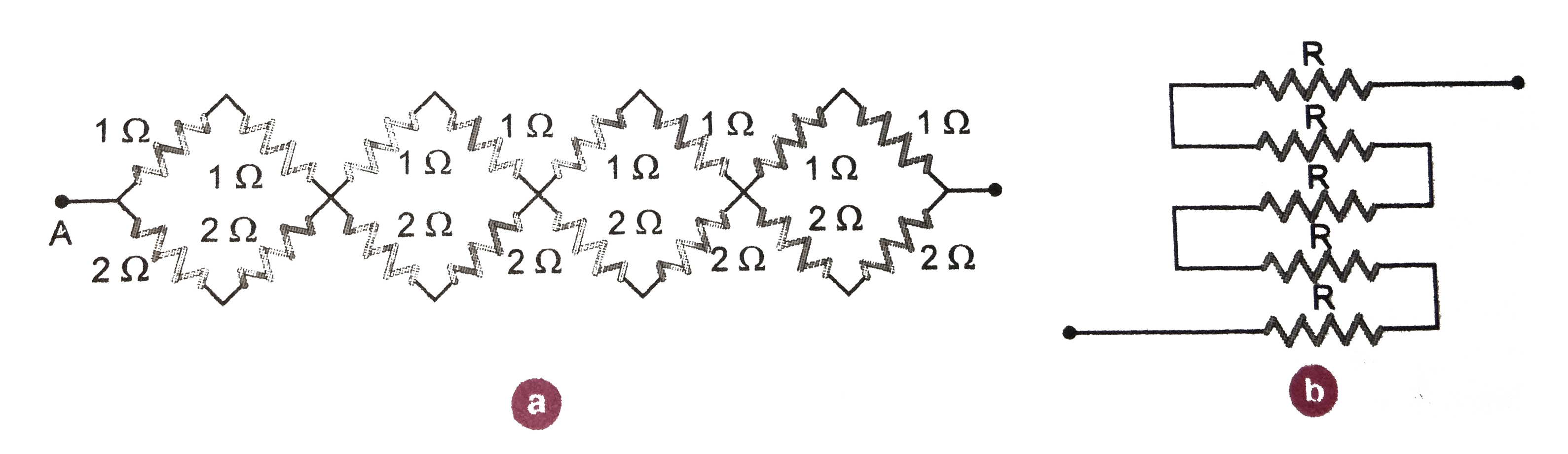 View Solution
View SolutionGiven n resistors each of resistance R, how will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View SolutionGiven n resistors each of resistane R, how will you combine them to get the (i) maximum, (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
View SolutionIdnetical resistor each of resistance r are connected as shown in figure. Calculate equivalent resistance between A and E.
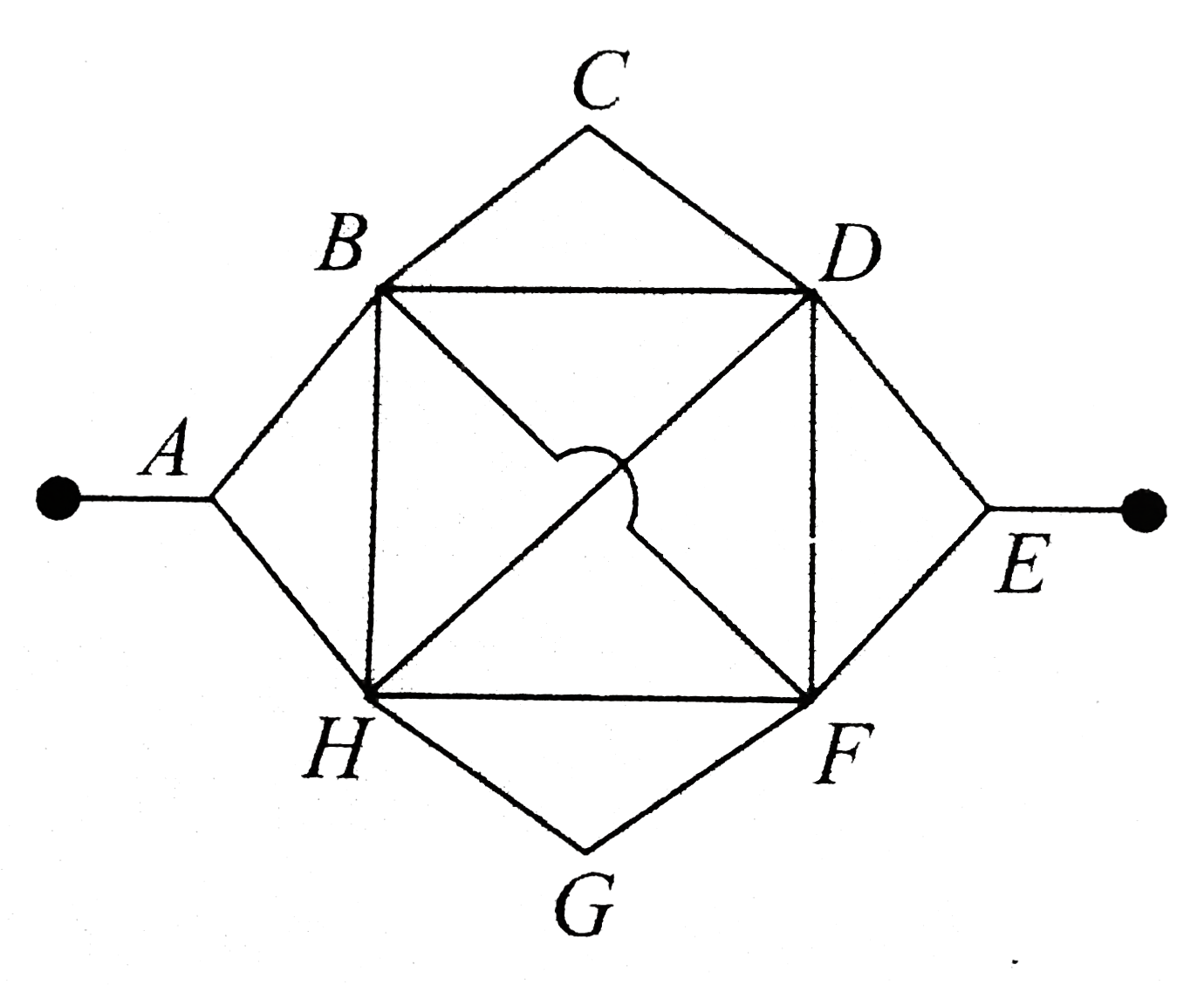 View Solution
View SolutionIf n resistors each of resistance r are connected to get (i) maximum possible resistance (ii) minimum possible resistance. Compute the ratio between values of resistances obtained in (i) and (ii).
View Solution

