A long straight wire of circular cross-section (radius a) is carrying steady current I. The current I is uniformly distributed across this cross-section. The magnetic field is
inversely proportional to r in the region and uniform throughout in the region
directly proportional to r in the region and inversely proportional to r in the region
zero in the region and inversely proportional to r in the region
uniform in the region r lt a and inversely proportional to distance r from the axis, in the region
The correct Answer is:B
To solve the problem of finding the magnetic field around a long straight wire of circular cross-section carrying a steady current I, we will use Ampère's Law and the concept of magnetic fields in cylindrical symmetry.
1. Understanding the Setup:
- We have a long straight wire with a circular cross-section of radius a.
- The current I is uniformly distributed across this cross-section.
2. Magnetic Field Inside the Wire (r < a):
- For points inside the wire (where the distance r from the center of the wire is less than the radius a), we can use Ampère's Law.
- The magnetic field B inside the wire can be given by the formula:
B=μ0Ienc2πr
- Here, Ienc is the current enclosed by the Amperian loop of radius r. Since the current is uniformly distributed, we can find Ienc as:
Ienc=I⋅r2a2
- Substituting this into the equation for B:
B=μ0(I⋅r2a2)2πr=μ0Ir2πa2
- This shows that the magnetic field B inside the wire is directly proportional to r.
3. Magnetic Field Outside the Wire (r > a):
- For points outside the wire (where the distance r is greater than the radius a), the entire current I flows through any Amperian loop we consider.
- The magnetic field B outside the wire can be expressed as:
B=μ0I2πr
- This indicates that the magnetic field B outside the wire is inversely proportional to r.
4. Conclusion:
- Thus, we summarize:
- For r<a: B∝r (directly proportional)
- For r>a: B∝1r (inversely proportional)
Final Answer:
- The magnetic field is directly proportional to r when r<a and inversely proportional to r when r>a.
- We have a long straight wire with a circular cross-section of radius a.
- The current I is uniformly distributed across this cross-section.
- For points inside the wire (where the distance r from the center of the wire is less than the radius a), we can use Ampère's Law.
- The magnetic field B inside the wire can be given by the formula:
B=μ0Ienc2πr
- Here, Ienc is the current enclosed by the Amperian loop of radius r. Since the current is uniformly distributed, we can find Ienc as:
Ienc=I⋅r2a2
- Substituting this into the equation for B:
B=μ0(I⋅r2a2)2πr=μ0Ir2πa2
- This shows that the magnetic field B inside the wire is directly proportional to r.
- For points outside the wire (where the distance r is greater than the radius a), the entire current I flows through any Amperian loop we consider.
- The magnetic field B outside the wire can be expressed as:
B=μ0I2πr
- This indicates that the magnetic field B outside the wire is inversely proportional to r.
- Thus, we summarize:
- For r<a: B∝r (directly proportional)
- For r>a: B∝1r (inversely proportional)
- The magnetic field is directly proportional to r when r<a and inversely proportional to r when r>a.
Topper's Solved these Questions
Similar Questions
Figure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 View Solution
View SolutionFigure shows a long straight wire of circular crosssection (radius a) carrying steady current I. The current I is uniformly distributed across this crosssection. Calculate the magnetic field in the region r<a and r>a.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A long straight wire of a circular cross-section (radius a) carries a steady current I and the current I is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance r from the centre of the wire?
A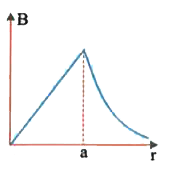 B
B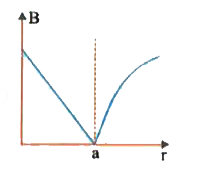 C
C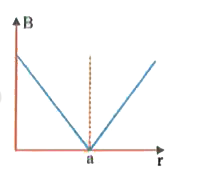 D
D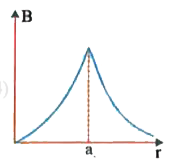
- Question 2 - Select One
A long straight wire of a circular cross section (radius a) carries a steady current 7 and the current / is uniformly distributed across this cross-section. Which of the following plots represents the variation of magnitude of magnetic field B with distance from the centre of the wire?
A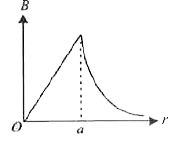 B
B C
C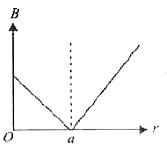 D
D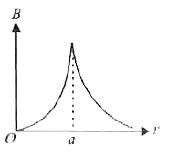
- Question 3 - Select One
The figure shows a long striaght wire of a circular cross-section (radius a) carrying steady current I.The current I is unifromly distributed across this distance a/2 and 2a from axis is
A2:1B1:2C4:1D1:1
The adjoining figure shows a long straight wire of a circular cross section (radius a) carrying steady current I. The current I is uniformly distributed across its cross section. Calculate the magnetic field at a distance from its axis for (i)r<a,(ii)r>a.
 View Solution
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View SolutionFigure show a long straight wire of a circular a cross-section with radius 'a' carrying steady curent I. The curent I is uniformaly distributed across this c ross -section.Calclulate the magnetic field in the regionr1<aandr2> a.
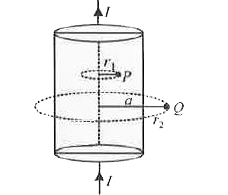 View Solution
View SolutionFigure shows a long straight wire of a circular cross-section (radius a) carrying steady current l. The current l is uniformly distributed across this cross-section. Calculate the magnetic field in the region r<aandr>a
 View Solution
View SolutionA long straight wire of a circular cross-section (radius r) carries a steady current I. The current is distributed uniformly across the cross-section. Calculare the magnetic field at a point (a) outside the wire , (b) inside the wire. Draw a graph showing variation of magnetic field.
View Solution

