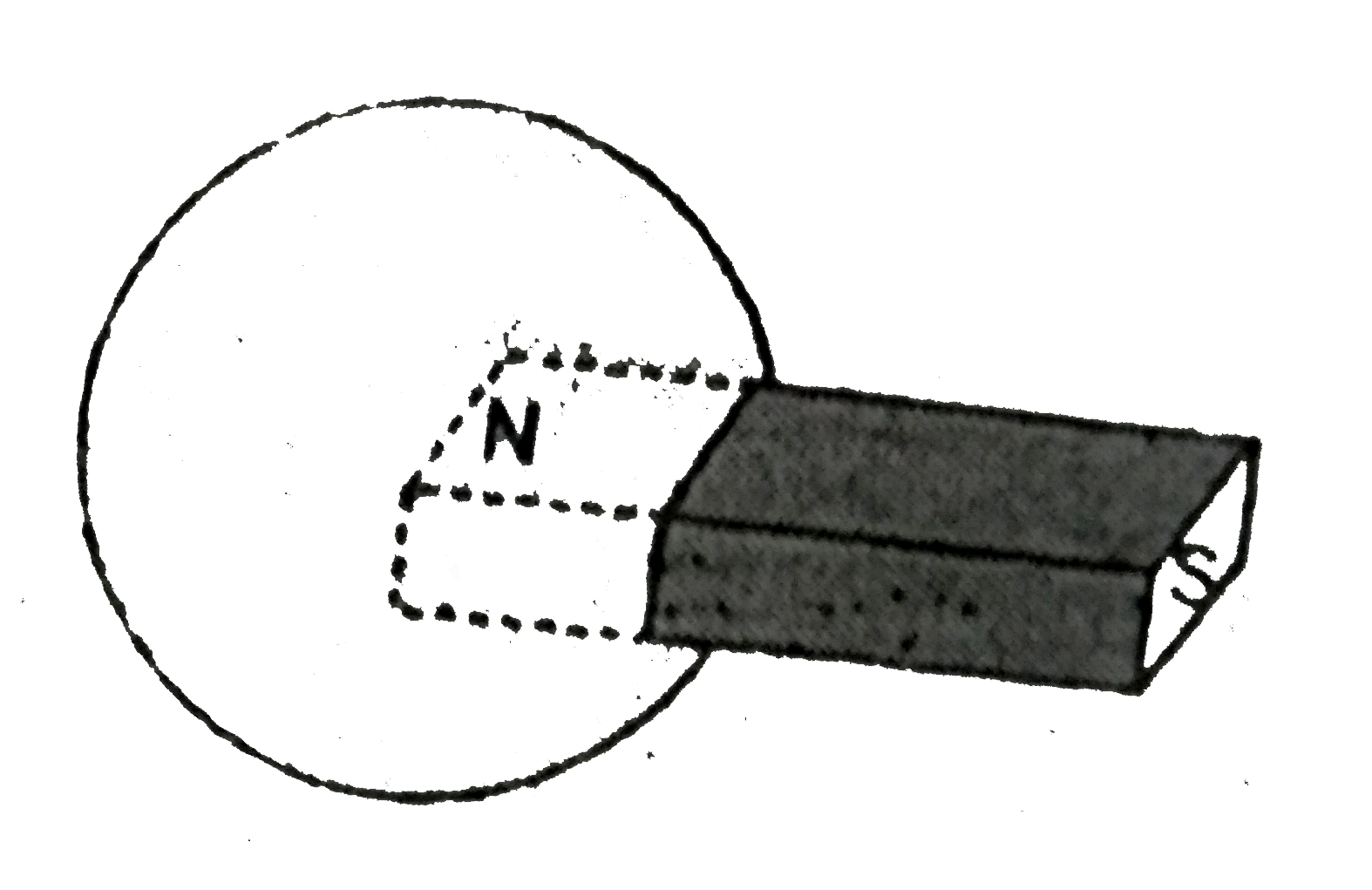
The net magnetic flux through any closed surface is :

Positive

Infinity

Negative

Zero

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the question regarding the net magnetic flux through any closed surface, we can follow these steps:
1. Understanding Magnetic Flux:
Magnetic flux (Φ) through a surface is defined as the integral of the magnetic field (B) over that surface. Mathematically, it is expressed as:
$Φ = \int \to B \cdot d \to S$
where $d \to S$ is a differential area vector on the surface.
2. Applying Gauss's Law for Magnetism:
According to Gauss's Law for magnetism, the net magnetic flux through any closed surface is always zero. This is expressed as:
$\oint \to B \cdot d \to S = 0$
This law states that there are no magnetic monopoles; hence, magnetic field lines that enter a closed surface must also exit it.
3. Conclusion:
Since the net magnetic flux through any closed surface is zero, we conclude that:
$Net magnetic flux = 0$
Final Answer:
The net magnetic flux through any closed surface is zero.
---

Updated on:8/8/2024

The net magnetic flux through any closed surface, kept in a magnetic field is
Azero
B $\frac{μ_{0}}{4 π}$
C $4 π μ_{0}$
D $\frac{4 μ_{0}}{π}$
The net magnetic flux through any closed surface, kept in a magnetic field is
Azero
B $\frac{μ_{0}}{4 π}$
C $4 π μ_{0}$
D $\frac{4 μ_{0}}{π}$
If the net electric flux through a closed surface is zero, then we can infer
Ano net charge is enclosed by the surface
Buniform electric field exists within the surface
Celectric potential varies from point to point inside the surface
Dcharge is present inside the surface