Calculate the maximum acceleration of a moving car so that a body lying on the floor of the car remains stationary. The coefficient of static friction between the body and the floor is 0.15(g=10ms−2)
150ms−2
1.5ms−2
50ms−2
1.2ms−2
To solve the problem of calculating the maximum acceleration of a moving car so that a body lying on the floor of the car remains stationary, we will use the concept of static friction.
1. Understanding the Forces:
- When the car accelerates, the body inside experiences a pseudo force in the opposite direction due to inertia. For the body to remain stationary relative to the car, the static friction must be able to counteract this pseudo force.
2. Static Friction Force:
- The maximum force of static friction (F_friction) can be calculated using the formula:
Ffriction=μs⋅N
- Here, μs is the coefficient of static friction and N is the normal force. For a body resting on the floor of the car, the normal force is equal to the weight of the body, which is mg (where m is the mass of the body and g is the acceleration due to gravity).
3. Substituting the Normal Force:
- Therefore, we can rewrite the friction force as:
Ffriction=μs⋅mg
4. Setting Up the Equation:
- The maximum static friction force must equal the force required to keep the body stationary in the accelerating car. This force can be expressed as:
F=ma
- Where a is the acceleration of the car. Setting these two forces equal gives us:
ma=μs⋅mg
5. Canceling Mass:
- Since the mass m appears on both sides of the equation, we can cancel it out (assuming m≠0):
a=μs⋅g
6. Substituting Values:
- Now, we can substitute the given values into the equation. We know:
- μs=0.15
- g=10m/s2
- Thus:
a=0.15⋅10=1.5m/s2
7. Final Answer:
- The maximum acceleration of the car so that the body remains stationary is:
a=1.5m/s2
- When the car accelerates, the body inside experiences a pseudo force in the opposite direction due to inertia. For the body to remain stationary relative to the car, the static friction must be able to counteract this pseudo force.
- The maximum force of static friction (F_friction) can be calculated using the formula:
Ffriction=μs⋅N
- Here, μs is the coefficient of static friction and N is the normal force. For a body resting on the floor of the car, the normal force is equal to the weight of the body, which is mg (where m is the mass of the body and g is the acceleration due to gravity).
- Therefore, we can rewrite the friction force as:
Ffriction=μs⋅mg
- The maximum static friction force must equal the force required to keep the body stationary in the accelerating car. This force can be expressed as:
F=ma
- Where a is the acceleration of the car. Setting these two forces equal gives us:
ma=μs⋅mg
- Since the mass m appears on both sides of the equation, we can cancel it out (assuming m≠0):
a=μs⋅g
- Now, we can substitute the given values into the equation. We know:
- μs=0.15
- g=10m/s2
- Thus:
a=0.15⋅10=1.5m/s2
- The maximum acceleration of the car so that the body remains stationary is:
a=1.5m/s2
Topper's Solved these Questions
Similar Questions
Detrmine the maximum acceleration of the train in which a box lying on the floor will remain stationary given that the coefficient of static friction between the box and the train s floor is 0.15 given g=10m/s2 .
View SolutionDetermine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary, given that the coefficient of static friction between the box and truck's floor is 0.2.
View Solution
Knowledge Check
Determine the maximum acceleration of the train in , which a box lying on its floor will remain stationary, given that the coefficient of static friction between the -box and the train floor is 0.15 (given g=10m/s2)
A1m/s2B1.5m/s2C2m/s2D0Maximum acceleration of the train in which a 50 kg box lying on its floor will ramain stationary is (Given: Co-efficient of static friction between the box and the train's floor is 0.3andg=10ms−2)
A5.0ms−2B3.0ms−2C1.5ms−2D15ms−2A box of mass 2 kg is placed on the roof of a car. The box would remain stationary until the car attains a maximum acceleration. Coefficient of static friction between the box and the roof of the car is 0.2 and 1g=10 ms−2.
The maximum acceleration of the car, for the box to remain stationary, isA8 ms−2B6 ms−2C4 ms−2D2 ms−2
Determine the maximum acceleration of the truck in which a box lying on the floor of its back will remain stationary , given that the coefficient of stastic friction between the box and trucks 's floor is 0⋅2 .
View SolutionA box of mass 2 kg is placed on the roof of a car. The box would remain stationary untill the car attains a maximum acceleration. Coefficient of static friction between the box and the roof of the car is 0.2 and g = 10ms−2. This maximum acceleration of the car, for the box to remain stationary, is
View SolutionWhen a maximum force of 3 N is applied on a body kept on rough inclined plane of shown in the figure, then body remains stationary. The maximum external force up the inclined plane that does not move the block is 12 N. The coefficient of static friction between the block and the plane is [Take, g = 10 m/s2]

View SolutionA car begains from rest at time t=0, and then acceleration along a straight track during the interval 0<t≤2s and thereafter with constant velocity as shown in figure in the graph. A coin is initially at rest on the floor of the car. At t=1s, the coin begains to slip and its stops slipping at t=3s . The coefficient of static friction between the floor and the coin is (g=10m/s2)
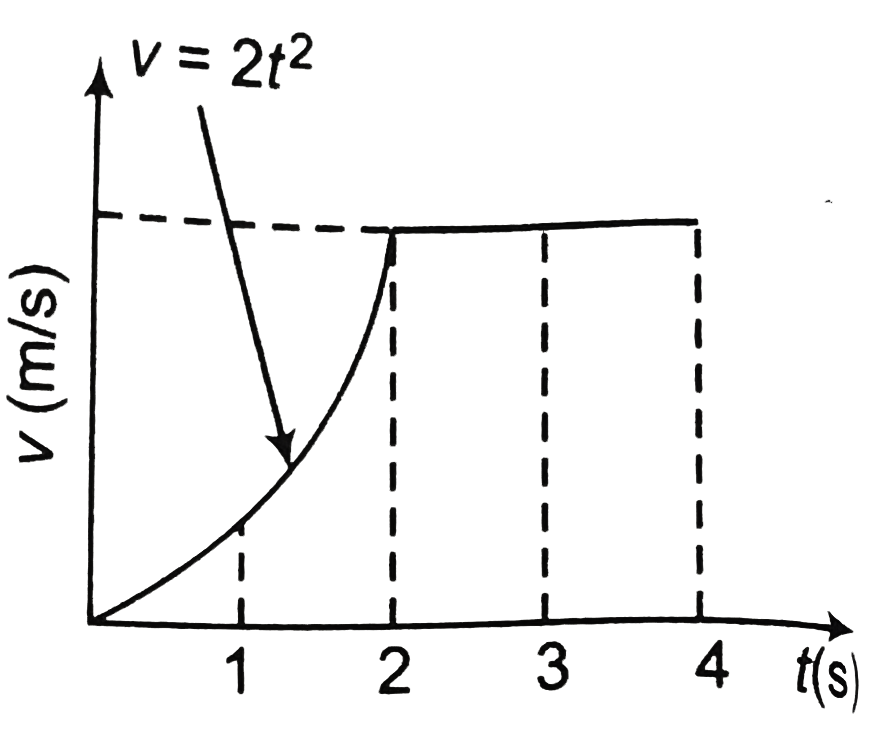
View SolutionMaximum acceleration of the train in which a box lying on its floor will ramain stationary, is
[μs=0.15,g=10m/s2]
View Solution
