Given below are two statements:
Statement I:The equivalent resistance of resistors in a series combination is smaller than least resistance used in the combination.
Statement II:The resistivity of the material is independent of temperature.
In the light of the above statements, choose the correct answer from the options given below:
Both Statement I and Statement II are false
Both Statement I and Statement II are true
Statement I is true but Statement II is false
Statement I is false but Statement II is true
To solve the question regarding the two statements, we will analyze each statement separately and determine their validity.
Step 1: Analyze Statement I
Statement I: The equivalent resistance of resistors in a series combination is smaller than the least resistance used in the combination.
In a series combination of resistors, the equivalent resistance Ra is given by the formula:
Ra=R1+R2+R3+…
This means that the equivalent resistance is the sum of all individual resistances. Therefore, the equivalent resistance Ra will always be greater than the smallest individual resistance in the combination.
Conclusion for Statement I: This statement is false.
Step 2: Analyze Statement II
Statement II: The resistivity of the material is independent of temperature.
The resistivity ρ of a material typically changes with temperature. For most conductors, resistivity increases with an increase in temperature, and this relationship can be expressed as:
ρ=ρ0(1+αΔT)
where ρ0 is the resistivity at a reference temperature, α is the temperature coefficient of resistivity, and ΔT is the change in temperature. This indicates that resistivity is dependent on temperature.
Conclusion for Statement II: This statement is false.
Final Conclusion
Both statements are false. Therefore, the correct answer is that both Statement I and Statement II are incorrect.
Summary of the Solution
- Statement I: False (Equivalent resistance in series is greater than any individual resistance).
- Statement II: False (Resistivity is dependent on temperature).
Statement I: The equivalent resistance of resistors in a series combination is smaller than the least resistance used in the combination.
Ra=R1+R2+R3+…
This means that the equivalent resistance is the sum of all individual resistances. Therefore, the equivalent resistance Ra will always be greater than the smallest individual resistance in the combination.
Statement II: The resistivity of the material is independent of temperature.
ρ=ρ0(1+αΔT)
where ρ0 is the resistivity at a reference temperature, α is the temperature coefficient of resistivity, and ΔT is the change in temperature. This indicates that resistivity is dependent on temperature.
Both statements are false. Therefore, the correct answer is that both Statement I and Statement II are incorrect.
- Statement I: False (Equivalent resistance in series is greater than any individual resistance).
- Statement II: False (Resistivity is dependent on temperature).
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Select the incorrect statement from the option given below.
AThe boiling point of alcohols and phenols are higher in comparison to hydrocarbons, ethers, haloalkanes and haloarenes of comparable molecular massesBEthanol and propane have comparable boiling points but differ only in the molecular massesCThe -OH group in alcohols and phenols is involved in the intermolecular hydrogen bondingDNone of the above - Question 2 - Select One
Match the following and choose the correct combination from the options given below
 AA=1, B=5, C=4, D=3, E=2BA=5, B=4, C=1, D=2, E=3CA=2, B=1, C=5, D=4, E=3DA=3, B=2, C=1, D=5, E=4
AA=1, B=5, C=4, D=3, E=2BA=5, B=4, C=1, D=2, E=3CA=2, B=1, C=5, D=4, E=3DA=3, B=2, C=1, D=5, E=4 - Question 3 - Select One
Match the following and choose the correct combination from the option given below:
 AA = 3, B = 4, C = 2, D = 1BA = 4, B = 3, C = 2, D = 1CA = 2, B = 3, C = 24 D = 1DA = 1, B = 4, C = 2, D = 3
AA = 3, B = 4, C = 2, D = 1BA = 4, B = 3, C = 2, D = 1CA = 2, B = 3, C = 24 D = 1DA = 1, B = 4, C = 2, D = 3
Match the following and choose the correct combination from the options given below.
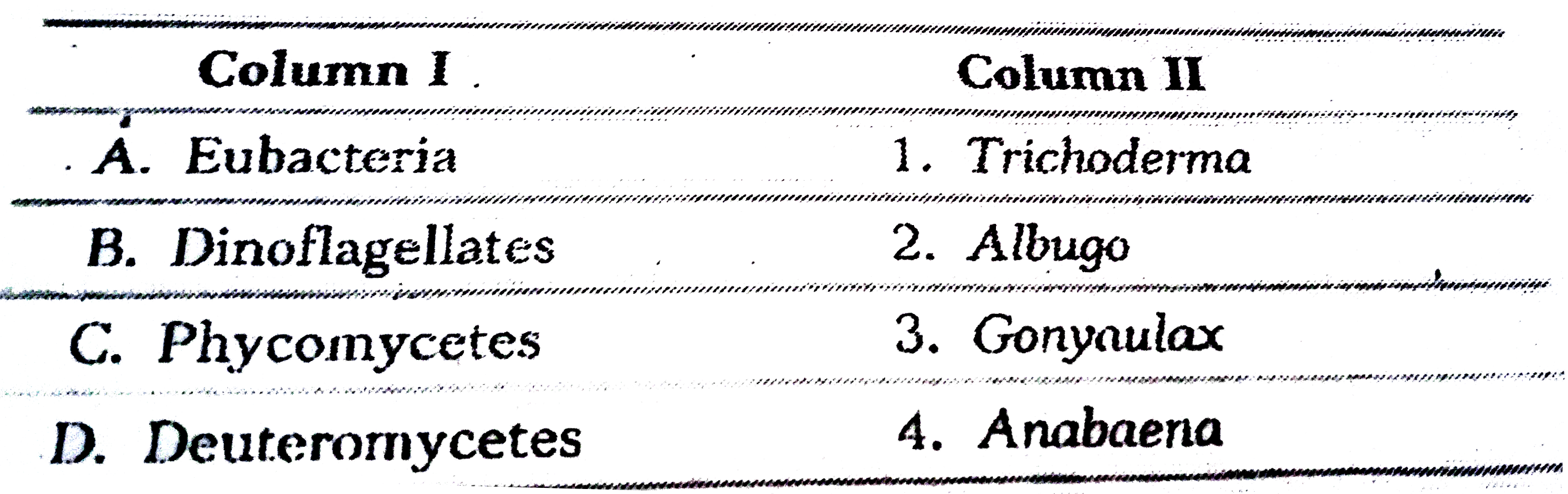 View Solution
View SolutionWhich of the following statements is not correct ? Choose the correct options from the given below.
View SolutionWhich of the following statements is not correct ? Choose the correct options from the given below.
View SolutionMatch the following and choose the correct combination from the option given below:
 View Solution
View SolutionMatch the column I and II, and choose the correct combination from the options given
 View Solution
View Solution


