Two identical particles each of mass 'm' go round a circle of radius a under the action of their mutual gravitational attraction.The angular speed of each particle will be:
√Gm4a3
√Gm2a3
√Gm8a3
√Gma3
To find the angular speed of each particle in the given scenario, we can follow these steps:
Step 1: Understand the System
We have two identical particles, each of mass m, moving in a circular path of radius a due to their mutual gravitational attraction. The distance between the two particles is 2a since they are on opposite sides of the circle.
Step 2: Write the Gravitational Force
The gravitational force F between the two particles can be expressed using Newton's law of gravitation:
F=Gm2(2a)2=Gm24a2
where G is the gravitational constant.
Step 3: Apply Centripetal Force Requirement
For circular motion, the required centripetal force Fc for each particle is given by:
Fc=mω2r
where r is the radius of the circular path (which is a for each particle) and ω is the angular speed.
Step 4: Set the Forces Equal
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal:
Gm24a2=mω2a
Step 5: Simplify the Equation
We can simplify this equation by canceling one m from both sides:
Gm4a2=ω2a
Now, rearranging gives:
ω2=Gm4a3
Step 6: Solve for Angular Speed
Taking the square root of both sides, we find the angular speed ω:
ω=√Gm4a3
Final Answer
Thus, the angular speed of each particle is:
ω=√Gm4a3
---
We have two identical particles, each of mass m, moving in a circular path of radius a due to their mutual gravitational attraction. The distance between the two particles is 2a since they are on opposite sides of the circle.
The gravitational force F between the two particles can be expressed using Newton's law of gravitation:
F=Gm2(2a)2=Gm24a2
where G is the gravitational constant.
For circular motion, the required centripetal force Fc for each particle is given by:
Fc=mω2r
where r is the radius of the circular path (which is a for each particle) and ω is the angular speed.
Since the gravitational force provides the necessary centripetal force, we can set these two forces equal:
Gm24a2=mω2a
We can simplify this equation by canceling one m from both sides:
Gm4a2=ω2a
Now, rearranging gives:
ω2=Gm4a3
Taking the square root of both sides, we find the angular speed ω:
ω=√Gm4a3
Thus, the angular speed of each particle is:
ω=√Gm4a3
Topper's Solved these Questions
Similar Questions
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Two identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is :
A√G2R3B12√GR3C12R√1GD√2GR3Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmRFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2)
Four particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
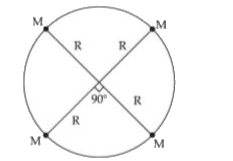
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View SolutionFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
View SolutionTwo particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitaitonal attraction. The speed of each particle with respect to their centre of a mass is -
View Solution
