As per given figure A,B and C are the first,second and third excited energy levels hydrogen atom respectively. If the ratio of the two wavelengths (ie. λ1//λ2) is 74n then the value of n will be

Step by step video solution for As per given figure A,B and C are the first,second and third excited energy levels hydrogen atom respectively. If the ratio of the two wavelengths (ie. lambda_1//lambda_2) is 7/(4n) then the value of n will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
In the hydrogen atom spectrum, λ3−1andλ2−1 represent wavelengths emitted due to transition from second and first excited states to the ground state respectively . The ratio λ3−1λ2−1=pq, where p and q are the smallest positive integers . What is the value of ( p + q ) ?
View SolutionTwo metal spheres have radii rand 2r and they emit thermal radiation with maximum intensities at wavelengths λ and 2λ. respectively. The respective ratio of the radiant energy emitted by them per second will be
View Solution
Knowledge Check
- Question 1 - Select One
Some energy levels of a molecule are shown in the figure. The ratio of the wavelengths r=λ1/λ2 is given by -
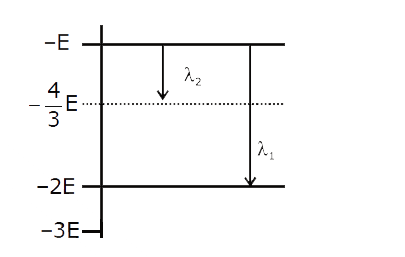 Ar=13Br=43Cr=23Dr=34
Ar=13Br=43Cr=23Dr=34 - Question 2 - Select One
Some energy levels of a molecule are shown in the fig. The ratio of the wavelengths r=λ1/λ2, is given by
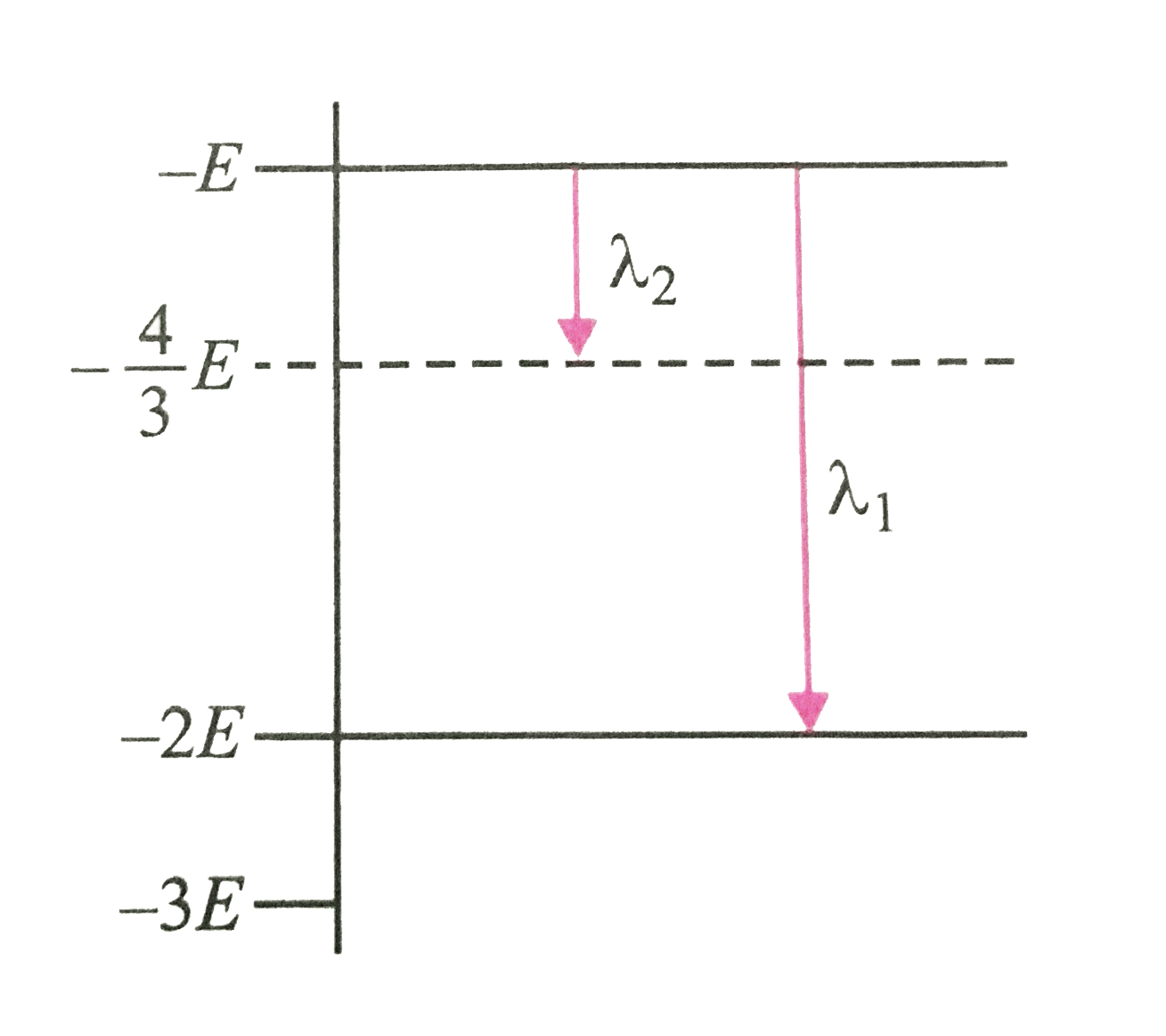 Ar=34Br=13Cr=43Dr=23
Ar=34Br=13Cr=43Dr=23 - Question 3 - Select One
If λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
A1:2:3B1:3:5C1:1/2:1/3D1:1/3:1/5
The shortest wavelength of the spectrum for transition of an electron to n=4energy level of a hydrogen like atom(atomic number = Z) is the same as the shortest wavelength of the Balmer series of hydrogen atom.The value of Z is:
View SolutionElectron in hydrogen atom first jumps from third excited state to second excited state and then form second excited state to first excited state. The ratio of wavelength λ1:λ2 emitted in two cases is
View SolutionIf λ1andλ2 , are the wavelengths of the third member of Lyman and first member of the Paschen series respectively, then the value of λ1:λ2 is:
View SolutionIf λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
View SolutionIf λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
View Solution

