If and area of is S and a parallelogram with sides parallel to and and diagonal , has area equal to B, then is equal to_________
To solve the problem, we need to find the ratio BS, where S is the area of triangle OAC and B is the area of the parallelogram defined by the vectors →OA and →OC.
Step 1: Calculate the area of triangle OAC
The area S of triangle OAC can be calculated using the formula:
S=12|→OA×→OC|
Given that →OA=→a and →OC=→b, we have:
S=12|→a×→b|
Step 2: Understand the parallelogram formed by →OA and →OC
The area B of the parallelogram formed by →OA and →OC is given by:
B=|→OA×→OC|
Thus, substituting for →OA and →OC:
B=|→a×→b|
Step 3: Relate the diagonal to the sides of the parallelogram
The diagonal →OB is given as:
→OB=12→a+4→b
From the properties of a parallelogram, the diagonal can be expressed in terms of the sides →OA and →OC:
→OB=→OA+→OC(one diagonal)
If we denote the sides of the parallelogram as →u=→OA and →v=→OC, the other diagonal can be expressed as:
→OB=→u+→vand→OB=→u−→v
Thus, we can write:
→u+→v=12→a+4→b
Step 4: Calculate the area of the parallelogram
The area B can also be calculated using the cross product of the sides:
B=|→u×→v|=|→a×→b|
However, since we have the diagonal, we can calculate the area of the parallelogram using:
B=12|→OB|2
Step 5: Find the ratio BS
Now, we have:
B=|→a×→b|andS=12|→a×→b|
Thus, the ratio BS becomes:
BS=|→a×→b|12|→a×→b|=2
Final Answer
The value of BS is 96.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If →A and →B denote the sides of a parallelogram and its area is AB/2 , the angle between →A and →B is :-
Aπ2BπCπ6Dπ3If OACB is a parallelogramwith −−→OC=→aand−−→AB=→b, then −−→OA=
A→a+→bB→q−→bC12(→b−→a)D12(→a−→b)If (→a×→b)2+(→a.→b)2 = 676 and ∣∣→b∣∣=2, then |→a| is equal to
A13B26C39Dnone of these
If −−→OA=2ˆi+3ˆj−4ˆkand−−→OB=ˆj+ˆk are two vectors through the origin O, find the projection of −−→OAand−−→OB
View SolutionIf E is the intersection point of diagonals of parallelogram ABCD and −−→OA+−−→OB+−−→OC+−−→OD=x−−→OE where O is origin then x=
View SolutionFind the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

View SolutionLet ABCD be a parallelogram whose diagonals intersect at P and let O be the origin. What is −−→OA+−−→OB+−−→OC+−−→OD equal to
View SolutionThe resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure is
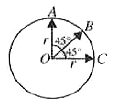
View Solution
