A coin is placed on a circular disc at a distance 'r', the friction coefficient between them is u, the maximum angular velocity with which the disc can rotate without slipping of coin
√2μgr
√μgr
√μgr
√3μgr
The correct Answer is:C
Topper's Solved these Questions
Similar Questions
A disc of radius 4 m is rotating about its fixed center with a constant angular velocity ω = 2 rad /s ( in the horizontal plane.) A bloc s also rotating with disc without slippng . If co- efficient of friction between the bloc and the disc is 0⋅4 then the maximum distance at which the block can rotate without slipping s ( g = 10m/s2) brgt
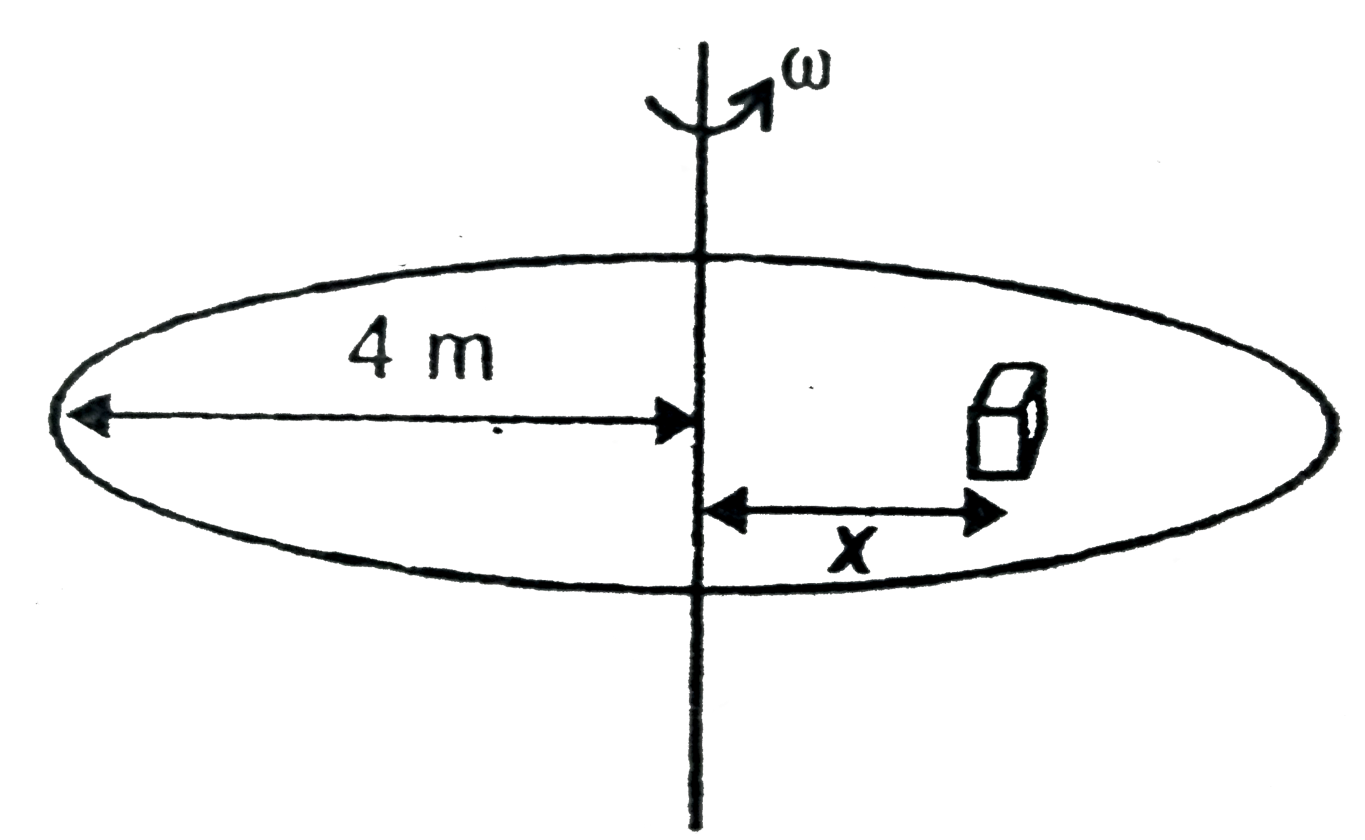
View SolutionA disc of radius 4m is rotating about its fixed centre with a constant angular velocity 2rads (in the horizontal plane).A block is also rotating with the disc without slipping. If co-efficient of friction between the block and the disc is 0.4 ,then the maximum distance at which the block can rotate without
View Solution
Knowledge Check
A coin is placed on a rotating platform at distance 'r' from its axis of rotation . To avoid the skidding of coin from rotating platform , the maximum angular velocity ω is
A√r/μgB√μg/rC√μrgDrgμA coin placed on a rotating table just slip when it is placed at a distance 4 r from the centre, on doubling the angular velocity of the table , the coin will just slip now the coin is at a distance from centre is
A4 rBr/4CrD2 rA disc of radius is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
A2cmB3cmC4 cmD6cm
A disc of radius 5 m is rotatating with angular frequency 10 rad/sec. A block of mass 2 kg is to be put on the disc frication coefficient between disc and block isμK=0.4, then find the maximum distance from axis where the block can be placed without slidding:
View SolutionA disc starts rotating with a constant angular acceleration of 1rad/s2 about a fixed vertical axis perpendicular to its plane and passing through its centre. A coin of mass 10gm is placed on the disc at a distance of 10cm from the axis. The coefficent of friction between the disc and the coin is 0.2. The value of the frictional force on the coin at t=1s will be
View SolutionA disc starts rotating with a constant angular acceleration of 1rad/s2 about a fixed vertical axis perpendicular to its plane and passing through its centre. A coin of mass 10gm is placed on the disc at a distance of 10cm from the axis. The coefficent of friction between the disc and the coin is 0.2. The value of the frictional force on the coin at t=1s will be
View SolutionA coin placed on a rotating gramophone disc, remains at rest when it is at a distance of 9 cm from its centre ,the angular velocity of the disc is then tripled .At what distance from the centre ,the coin should be placed , so that it will remain at rest ?
View SolutionA coins kept on a horizontal rotating disc has its centre at a distance of 0.25 m from the axis of rotation of the disc .If μis0.2, then the angular velocity of the disc at which the coion will slip off, (g=9.8m/s2)
View Solution
