Two charges "q" and "3q" are separated by a distance ' "r" ' in air. At a distance "x" from charge "q" ,the resultant electric field is zero.The value of "x" is :
(1+√3)r
r3(1+√3)
r(1+√3)
r(1+√3)
To solve the problem, we need to find the distance "x" from charge "q" where the resultant electric field is zero due to the two charges "q" and "3q" separated by a distance "r".
1. Understanding the Electric Field:
The electric field (E) due to a point charge is given by the formula:
E=k⋅|q|r2
where k is Coulomb's constant, q is the charge, and r is the distance from the charge.
2. Setting Up the Problem:
We have two charges:
- Charge q at point A (let's say at position 0)
- Charge 3q at point B (at position r)
We need to find a point P at a distance x from charge q where the electric field is zero.
3. Electric Field at Point P:
- The electric field due to charge q at point P (distance x):
Eq=k⋅qx2
- The electric field due to charge 3q at point P (distance r−x):
E3q=k⋅3q(r−x)2
4. Condition for Zero Electric Field:
For the resultant electric field to be zero at point P, the magnitudes of the electric fields due to both charges must be equal:
Eq=E3q
Thus, we have:
k⋅qx2=k⋅3q(r−x)2
5. Cancelling Common Terms:
We can cancel k and q from both sides (assuming q≠0):
1x2=3(r−x)2
6. Cross-Multiplying:
Cross-multiplying gives:
(r−x)2=3x2
7. Expanding the Equation:
Expanding the left side:
r2−2rx+x2=3x2
Rearranging gives:
r2−2rx−2x2=0
8. Using the Quadratic Formula:
This is a quadratic equation in x:
2x2+2rx−r2=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=2,b=−2r,c=−r2:
x=−(−2r)±√(−2r)2−4⋅2⋅(−r2)2⋅2
Simplifying gives:
x=2r±√4r2+8r24=2r±√12r24
x=2r±2√3r4=r(1±√3)2
9. Choosing the Correct Value of x:
Since x must be positive and less than r, we take:
x=r(1−√3)2
Final Answer:
x=r1+√3
The electric field (E) due to a point charge is given by the formula:
E=k⋅|q|r2
where k is Coulomb's constant, q is the charge, and r is the distance from the charge.
We have two charges:
- Charge q at point A (let's say at position 0)
- Charge 3q at point B (at position r)
- The electric field due to charge q at point P (distance x):
Eq=k⋅qx2
- The electric field due to charge 3q at point P (distance r−x):
E3q=k⋅3q(r−x)2
For the resultant electric field to be zero at point P, the magnitudes of the electric fields due to both charges must be equal:
Eq=E3q
Thus, we have:
k⋅qx2=k⋅3q(r−x)2
We can cancel k and q from both sides (assuming q≠0):
1x2=3(r−x)2
Cross-multiplying gives:
(r−x)2=3x2
Expanding the left side:
r2−2rx+x2=3x2
Rearranging gives:
r2−2rx−2x2=0
This is a quadratic equation in x:
2x2+2rx−r2=0
Using the quadratic formula x=−b±√b2−4ac2a:
Here, a=2,b=−2r,c=−r2:
x=−(−2r)±√(−2r)2−4⋅2⋅(−r2)2⋅2
Simplifying gives:
x=2r±√4r2+8r24=2r±√12r24
x=2r±2√3r4=r(1±√3)2
Since x must be positive and less than r, we take:
x=r(1−√3)2
x=r1+√3
Topper's Solved these Questions
Similar Questions
Two charge _q and -3q are placed at a distance of 1 m apart.Find out the points on the line joing two charges, where electric potential is zero.
View SolutionTwo point charges, q1=10×10−8Candq2=−2×10−8C, are separated by a distance of 60 cm in air.
Find at what distance from the 1st charge q1, would the electric potential be zero.
View Solution
Knowledge Check
Two point charges Q and −Q/4 are separated by a distance X. Then
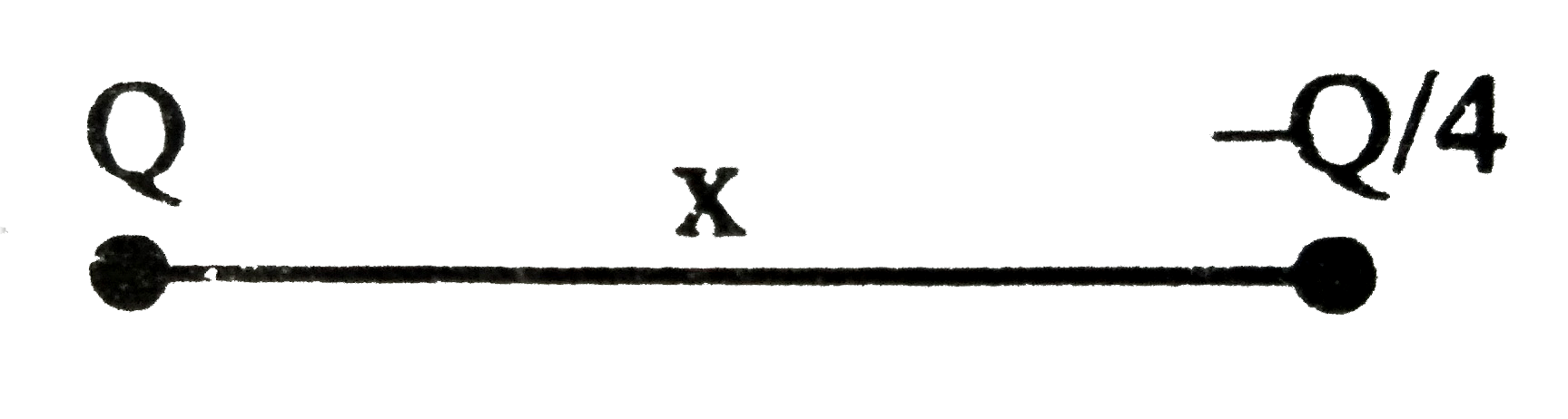.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Two charges +4e and +e are at a distance x apart. At what distance,a charge q must be placed from charge +e so that is in equilibrium
Ax/2B2x/3Cx/3Dx/6Two charges e and 3e are placed at a distance r. The distance of the point where the electric field intensity will be zero is
Ar(1+√3) from 3e chargeBr(1+√3) from e chargeCr(1−√3) from 3e chargeDr1+√13 from e charge
Two point charges q and −q are separated by the distance l, both being located at a distance l/2 from the infinite conducting plane. Find :
(a) the modulus of the electric force acting on each charge,
(b) the magnitude of the electric field strength vector at the midpoint between these charges.
View SolutionTwo charges +9e and +e are at a distance x a part.At what distance, a charge q must be placed from charge +e so that it is in equilibrium
View SolutionTwo point charges q and −q are separated by the distance 2l. Find the flux of the electric field strength vector across a circle of radius R.
View SolutionTwo point charges q and -q are separated by a distance 2a. Evaluate the flux of the electric field strength vector across a circle of radius R.
View SolutionTwo positive point charges q1=16μC and q2=4μC are separated in vacuum by a distance of 3.0m. Find the point on the line between the charges where the net electric field is zero.-
View Solution