A coin is placed on a disc.The coefficient of friction between the coin and the disc is μ .If the distance of the coin from the center of the disc is "r" ,the maximum angular velocity which can be given to the disc,so that the coin does not slip away, is:
μ√rg
μgr
√μgr
√rμg
To solve the problem of finding the maximum angular velocity (ωmax) that can be given to the disc so that the coin does not slip, we can follow these steps:
Step 1: Understand the Forces Acting on the Coin
The forces acting on the coin placed on the disc are:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting upwards.
- The frictional force (f) acting towards the center of the disc, which provides the necessary centripetal force to keep the coin in circular motion.
Step 2: Write the Expression for Centripetal Force
For the coin to remain in circular motion without slipping, the frictional force must provide the necessary centripetal force. The centripetal force (Fc) required for an object moving in a circle of radius r with angular velocity ω is given by:
Fc=mω2r
Step 3: Relate Frictional Force to Normal Force
The maximum frictional force (f) that can act on the coin before it starts slipping is given by:
f≤μN
where μ is the coefficient of friction and N is the normal force. Since the only forces acting vertically on the coin are the weight and the normal force, we have:
N=mg
Thus, the maximum frictional force can be expressed as:
fmax=μmg
Step 4: Set Up the Inequality for No Slipping Condition
For the coin to not slip, the centripetal force must be less than or equal to the maximum frictional force:
mω2r≤μmg
Step 5: Simplify the Inequality
We can cancel m from both sides (assuming m≠0):
ω2r≤μg
Step 6: Solve for Maximum Angular Velocity
Rearranging the inequality gives:
ω2≤μgr
Taking the square root of both sides, we find the maximum angular velocity:
ωmax=√μgr
Conclusion
Thus, the maximum angular velocity that can be given to the disc so that the coin does not slip away is:
ωmax=√μgr
The forces acting on the coin placed on the disc are:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting upwards.
- The frictional force (f) acting towards the center of the disc, which provides the necessary centripetal force to keep the coin in circular motion.
For the coin to remain in circular motion without slipping, the frictional force must provide the necessary centripetal force. The centripetal force (Fc) required for an object moving in a circle of radius r with angular velocity ω is given by:
Fc=mω2r
The maximum frictional force (f) that can act on the coin before it starts slipping is given by:
f≤μN
where μ is the coefficient of friction and N is the normal force. Since the only forces acting vertically on the coin are the weight and the normal force, we have:
N=mg
Thus, the maximum frictional force can be expressed as:
fmax=μmg
For the coin to not slip, the centripetal force must be less than or equal to the maximum frictional force:
mω2r≤μmg
We can cancel m from both sides (assuming m≠0):
ω2r≤μg
Rearranging the inequality gives:
ω2≤μgr
Taking the square root of both sides, we find the maximum angular velocity:
ωmax=√μgr
Thus, the maximum angular velocity that can be given to the disc so that the coin does not slip away is:
ωmax=√μgr
Topper's Solved these Questions
Similar Questions
A small mass m rests at the edge of a horizontal disc of radius R. The coefficient of static friction between the mass and the disc is μ. The disc is rotated about its axis at an angular velocity such that the mass slides off the disc and lands on the floor h metres below. The horizontal "distance of travel of the mass is : √kμRh. Find k.
View SolutionA unifrom disc of radius R, is resting on a table on its rim. The coefficient of friction between disc and table is μ Fig. Now the disc is spulled with a force F as shown in the Fig. What is the maximum value of F for which the disc rolls without slipping ?


View Solution
Knowledge Check
The coin is notating with a plate without sliding If the coefficient of friction between the coin and plane is μ=0.75 the friction between the coin and plate is

If the plate is rotating along and the coin is gently placed on the rotating plate, the frictional force on the coin isAmgB32mgCmg2D34mgThe coin is notating with a plate without sliding If the coefficient of friction between the coin and plane is μ=0.75 the friction between the coin and plate is

If the angular frequency of the rotation of the plate is ω=√g2R the friction force acting on coin isA34mg→Bmg4←C3mg4←Dmg2→A coins kept on a horizontal rotating disc has its centre at a distance of 0.25 m from the axis of rotation of the disc .If μis0.2, then the angular velocity of the disc at which the coion will slip off, (g=9.8m/s2)
A3.8rad/sB2.8rad/sC4.8rad/sD5.8rad/s
A small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of hte resultant force on the coin exerted by the disc just before it starts slipping on the disc is :

View SolutionThe coefficient of static friction between a small coin and the surface of a turntable is 0.30 . The turntable rotates at 2rads−1. What is maximum distance from the centre of the turntable at which the coin will not slide ?
View SolutionA disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.
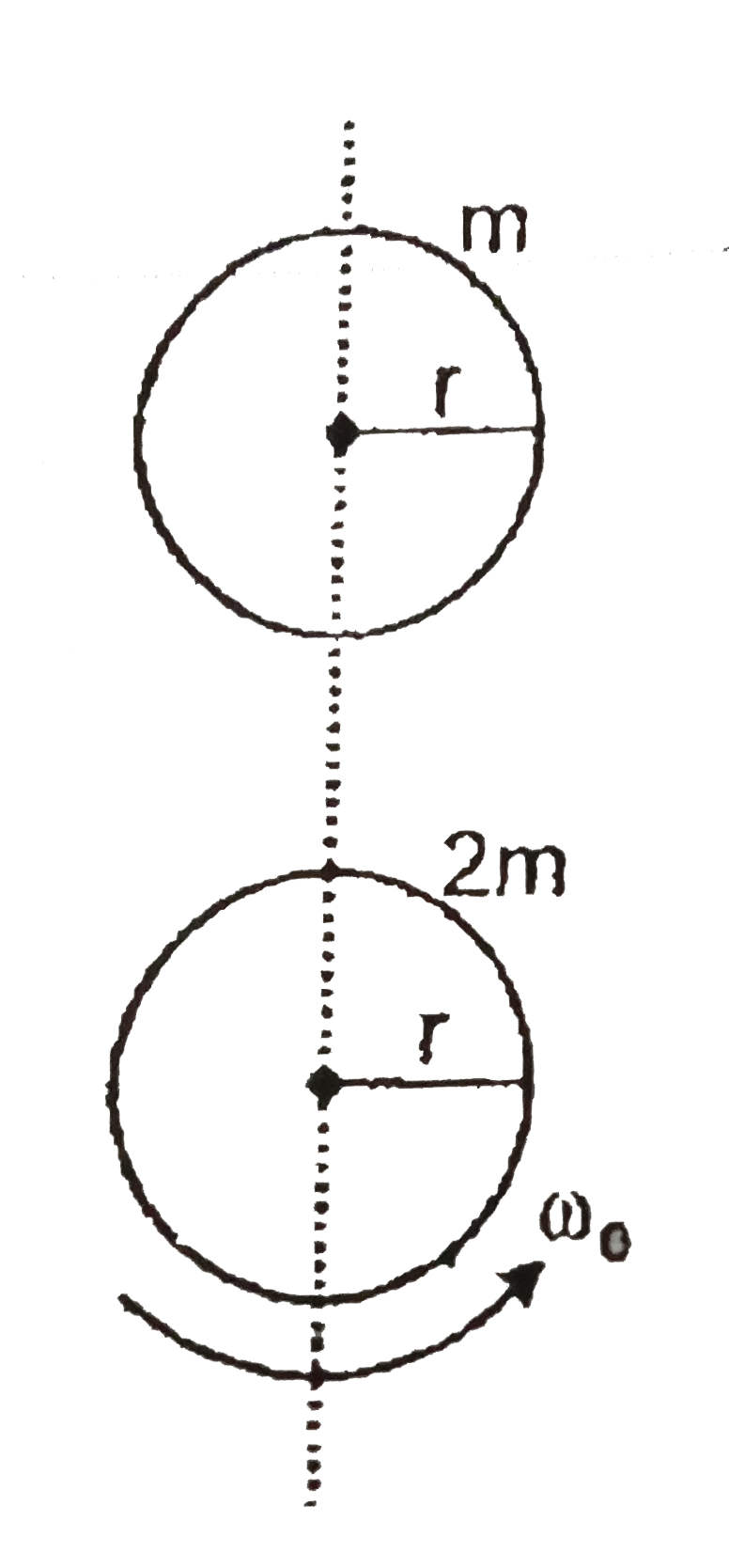
Angular velocity 'ω' when both discs start rotating together without slipping
View SolutionA coin is place at a distance 9 cm from centre on a rotating turn table slip. If the angular velocity of the turn table is tripled, then the distance ofn the coin from the centre will be
View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View Solution
