A disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.
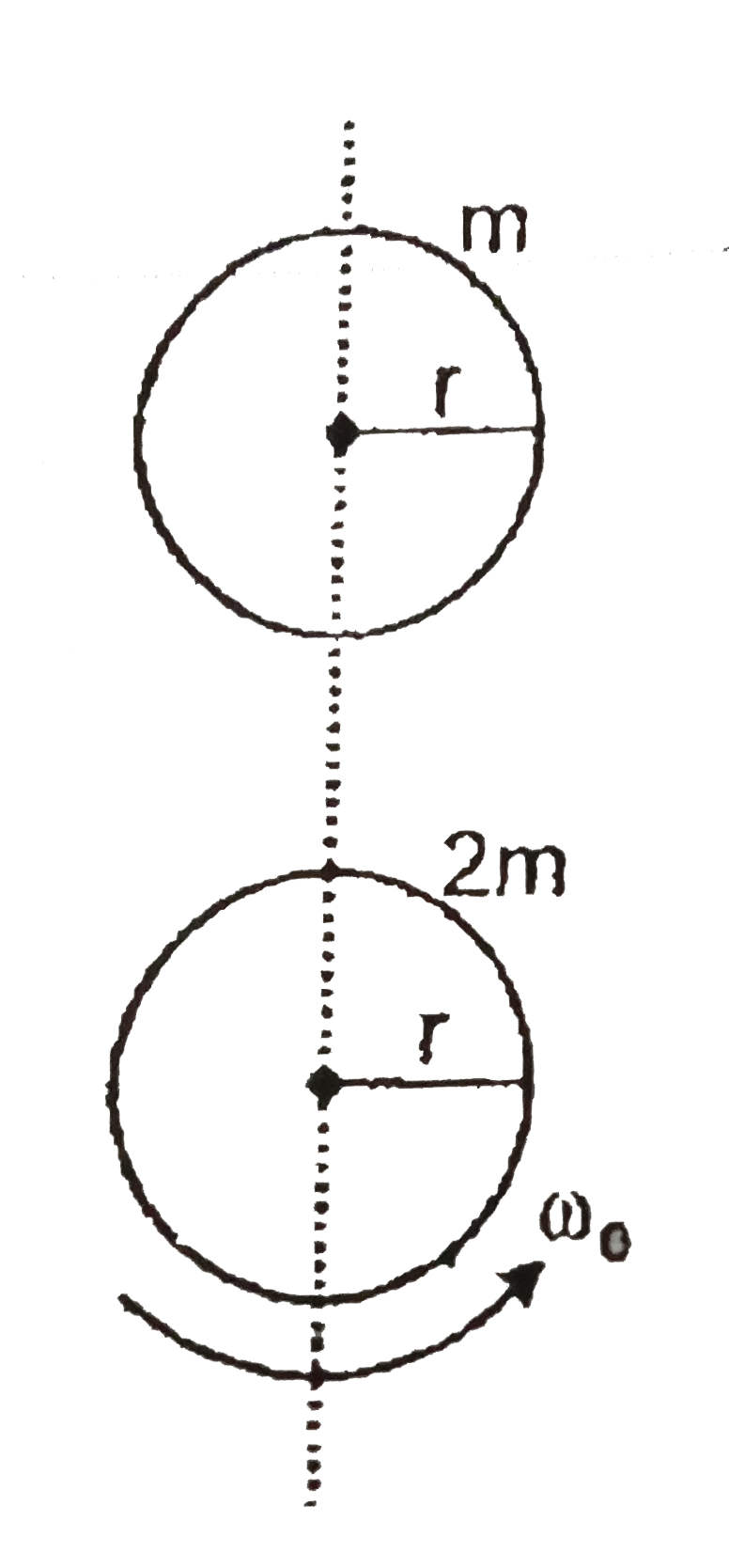
Angular velocity 'ω' when both discs start rotating together without slipping
2ω03
3ω04
ω03
ω02
The correct Answer is:B
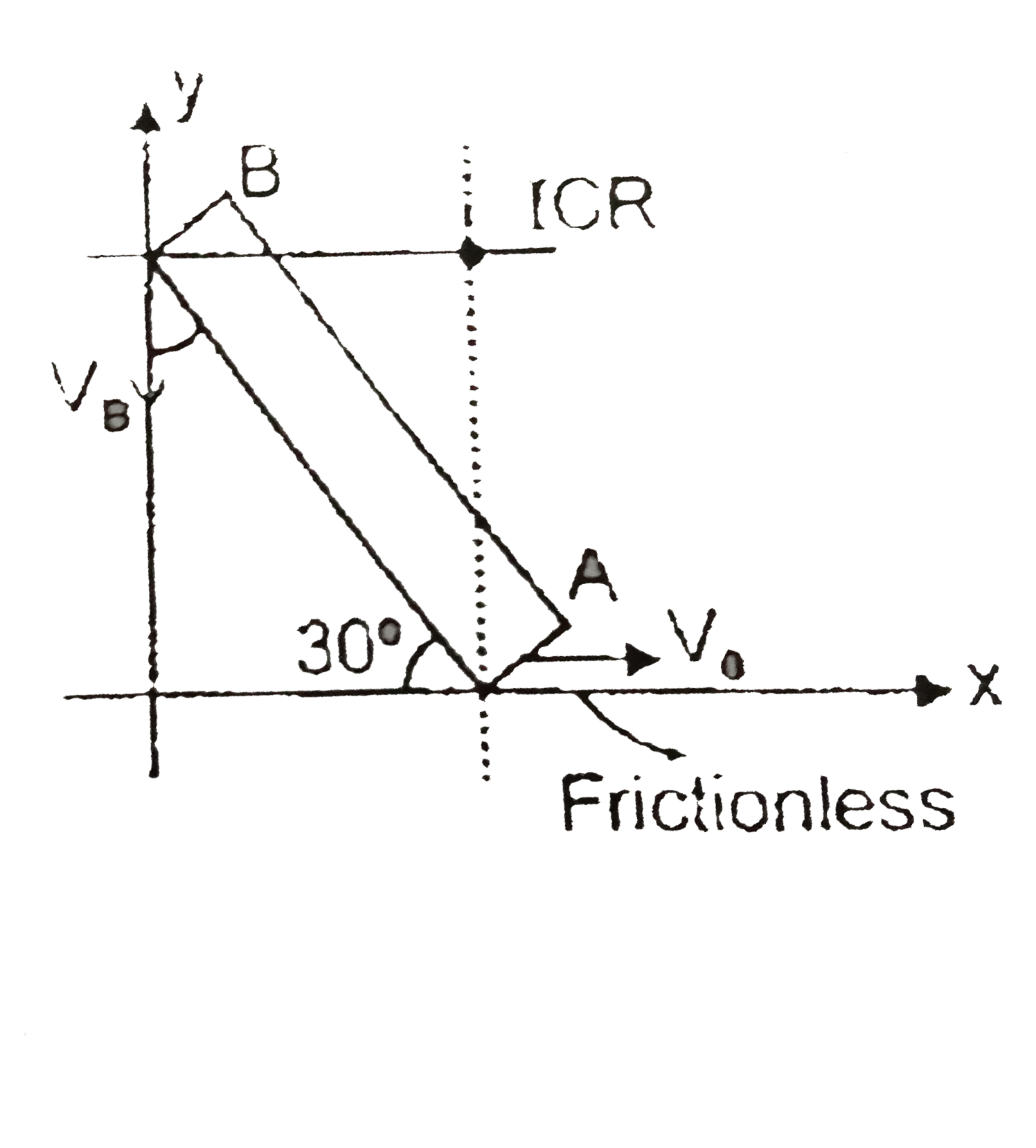
VB=ω(lcos30∘)
VA=ω(lsin30∘)=V0
⇒ω=2V0l
LICR=(I)ICRω
(I)ICR=Icm+md2=ml212+m(l2)2=ml23
(I)ICR=(ml23)(2v0l)=2mv0l3
Topper's Solved these Questions
Similar Questions
Out of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
View SolutionA disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View Solution
Knowledge Check
A disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.
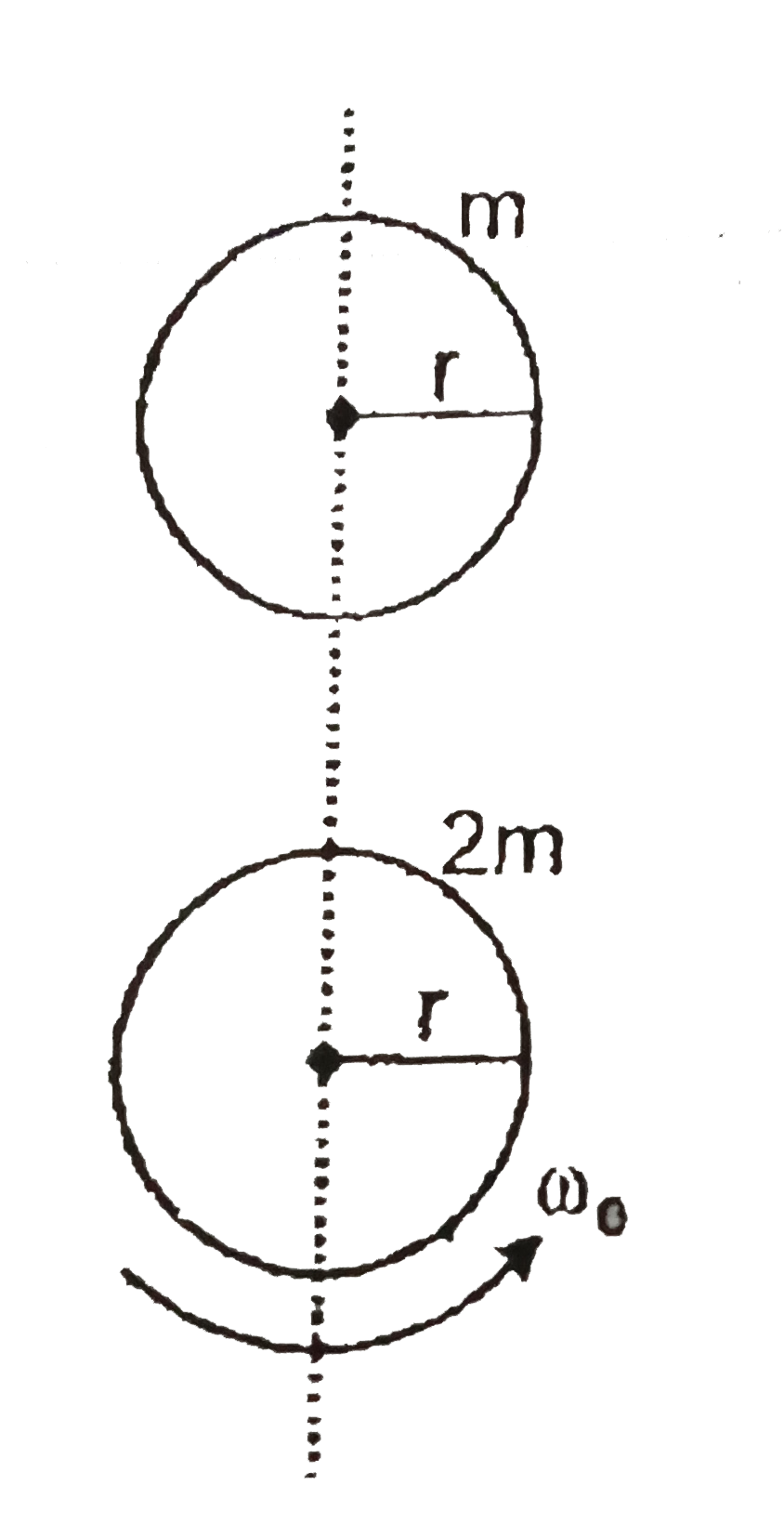
Time elapsed in this processAω0RμgB2ω0RμgCω0R2μgDω0R4μgA disc of mass m and radius r is gently placed on another disc of mass 2m and radius r. The disc of mass 2m is rotating with angular velocity ω0 initially.
The disc is placed such that axis of both are concident. The coefficient of friction is μ for surfaces of contact Assume that pressure on disc is uniformely distributed.

Loss in kinetic energy of systemA16mr2ω20B13mr2ω20C12mr2ω20DNone of theseA disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
AMRω4tBMRω2tCMRωtDMRωt
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionOut of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
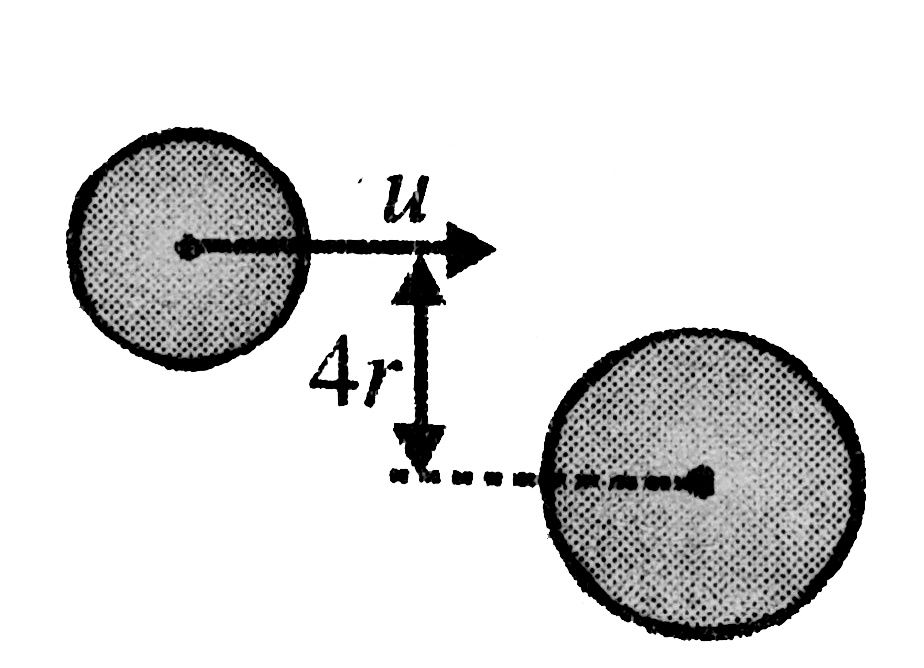 What is the final velocity of the heavier disc?
What is the final velocity of the heavier disc?
View SolutionA disc of mass m and radius r placed on a routh horizontal surface. A cue of mass m hits the disc at a height h from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
View Solution
