A uniform magnetic field of 2×10−3T acts along positive Y-direction. A rectangular loop of sides 20cm and 10cm with current of 5A is in Y−Z plane.The current is in anticlockwise sense with reference to negative X axis.Magnitude and direction of the torque is:
2×10−4N−m along positive Y−direction
2×10−4N−m along negative Z−direction
2×10−4N−m along positive Z−direction
2×10−4N−m along positive X−direction
To solve the problem, we will follow these steps:
Step 1: Identify the given parameters
- Magnetic field B=2×10−3T (along positive Y-direction)
- Dimensions of the rectangular loop: l=20cm=0.2m and w=10cm=0.1m
- Current I=5A
- The loop is in the Y-Z plane and the current flows anticlockwise with respect to the negative X-axis.
Step 2: Calculate the area vector of the loop
The area A of the rectangular loop can be calculated as:
A=l×w=0.2m×0.1m=0.02m2
Since the loop is in the Y-Z plane and the area vector points in the negative X-direction, we can represent the area vector as:
→A=−A^i=−0.02^im2
Step 3: Calculate the magnetic moment
The magnetic moment →m is given by the product of the current and the area vector:
→m=I→A=5A×(−0.02^i)=−0.1^iA⋅m2
Step 4: Calculate the torque on the loop
The torque →τ experienced by the loop in a magnetic field is given by the cross product of the magnetic moment and the magnetic field:
→τ=→m×→B
Substituting the values:
- →B=2×10−3^jT
Now, we calculate the cross product:
→τ=(−0.1^i)×(2×10−3^j)
Using the right-hand rule, we know:
^i×^j=^k
Thus:
→τ=−0.1×2×10−3^k=−2×10−4^kN⋅m
Step 5: Determine the magnitude and direction of the torque
The magnitude of the torque is:
|→τ|=2×10−4N⋅m
The direction of the torque is in the negative Z-direction (since it is −^k).
Final Answer
The magnitude of the torque is 2×10−4N⋅m and it acts in the negative Z-direction.
---
- Magnetic field B=2×10−3T (along positive Y-direction)
- Dimensions of the rectangular loop: l=20cm=0.2m and w=10cm=0.1m
- Current I=5A
- The loop is in the Y-Z plane and the current flows anticlockwise with respect to the negative X-axis.
The area A of the rectangular loop can be calculated as:
A=l×w=0.2m×0.1m=0.02m2
Since the loop is in the Y-Z plane and the area vector points in the negative X-direction, we can represent the area vector as:
→A=−A^i=−0.02^im2
The magnetic moment →m is given by the product of the current and the area vector:
→m=I→A=5A×(−0.02^i)=−0.1^iA⋅m2
The torque →τ experienced by the loop in a magnetic field is given by the cross product of the magnetic moment and the magnetic field:
→τ=→m×→B
Substituting the values:
- →B=2×10−3^jT
→τ=(−0.1^i)×(2×10−3^j)
Using the right-hand rule, we know:
^i×^j=^k
Thus:
→τ=−0.1×2×10−3^k=−2×10−4^kN⋅m
The magnitude of the torque is:
|→τ|=2×10−4N⋅m
The direction of the torque is in the negative Z-direction (since it is −^k).
The magnitude of the torque is 2×10−4N⋅m and it acts in the negative Z-direction.
Topper's Solved these Questions
Similar Questions
A uniform magnetic field of 3000G is established along the positive z-direction. A rectangular loop of sides 10cm and 5cm carries a current 12A. What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?

View SolutionA unform magnetic field of 3000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A . What is the torque on the loop in the different cases shown in the fig ? What is the force on each case? Which case corresponds to stable equilibrium ?
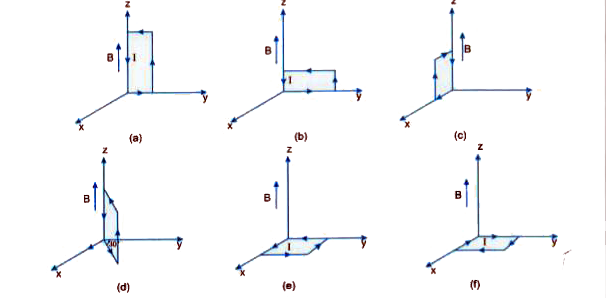
View Solution
Knowledge Check
A uniformi magnetic field of 3 T is established along the positive Z-direction. A rectangular loop in XY plane of sides 10 cm and 5 cm carries a current of 11 A as shown The torque on the loop is:
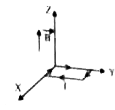 A+1.8×10−2ˆjNmB−1.8×10−2ˆjNmCZeroD−1.8×10−2ˆjNm
A+1.8×10−2ˆjNmB−1.8×10−2ˆjNmCZeroD−1.8×10−2ˆjNmA uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
 AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4NmA uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
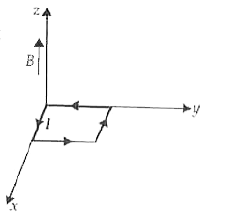 AzeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AzeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
A loop of wire having 50 turns carries a current of 10A in anticlockwise direction. If diameter of loop is 10cm, what is the magnitude and direction of magnetic moment of current loop?
View SolutionA circular loop of area 1cm2 carrying a current of 10A is placed in a magnetic field of 2Tˆi. The loop is in xy plane with current in clockwise direction . Fing the torque on the loop
View SolutionA uniform magnetic field B of0.3 T is along the positive Z-direction. A rectangular loop (abed) of sides 10cm×5cm carries a current I of 12 A. Out of the following different orientations which one corresponds to stable equilibrium?
View SolutionA rectangular loop of sides 20cm and 10cm carries a current of 5.0A. A uniform magnetic field of magnitude 2T exists parallel to the longer side of the loop. The torque acting on the loop is
View SolutionTwo Concentric circular coils X and Y of radii 16cm and 10cm lie in the same vertical plane containing N−S direction X has 20 turns and carries 16A.Y has 25 truns & carries 18A.X has current in anticlockwise direction and Y has current in clockwise direction for the observer, looking at the coils facing the west. The magnitude of net magnetic field at their common centre is .
View Solution
