The identical spheres each of mass 2M are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 4 m each. Taking point of intersection of these two sides as origin, the magnitude of position vector of the centre of mass of the system is 4√2x , where the value of x is ___________
The correct Answer is:3
Step by step video & text solution for The identical spheres each of mass 2M are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 4 m each. Taking point of intersection of these two sides as origin, the magnitude of position vector of the centre of mass of the system is frac{4 sqrt 2}{x} , where the value of x is ___________ by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Three identical spheres , each of mass M , are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 2 m . Taking their point of intersection as the origin , find the position vector of centre of mass
View SolutionFour particle, each of mass m, are placed at corners of a square of side a in the x-y plane. If the origin of the co-ordinate system is taken at the point fo intersection of the diagonals of the square, the co-ordinates of the centre of mass of the system are:
View Solution
Knowledge Check
- Question 1 - Select One
Three identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
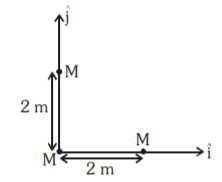 A(##PW_NEET_45_DAY_PHY_C06_E03_004_Q01##)B23(ˆi+ˆj)C43(ˆi+ˆj)D2(ˆi+ˆj)
A(##PW_NEET_45_DAY_PHY_C06_E03_004_Q01##)B23(ˆi+ˆj)C43(ˆi+ˆj)D2(ˆi+ˆj) - Question 2 - Select One
Three identical spheres each of mass M are placed at corners of right angle triangle with mutually perpendicular sides equal to 2m. Taking point of intersection of two mutually perpendicular sides as origin find position vector center of mass
 A2(ˆi+ˆj)B(ˆi+ˆj)C2ˆi+ˆj3D4ˆi+ˆj3
A2(ˆi+ˆj)B(ˆi+ˆj)C2ˆi+ˆj3D4ˆi+ˆj3 - Question 3 - Select One
Three equal masses each of 50 g, are placed at the corners of a right angled isoceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is
Ax=5 cm,y=5 cmBx=53 cm,y=5 cmCx=53 cm,y=52 cmDx=53 cm,y=53 cm
Three identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionFour identical spheres each of mass m are placed at the corner of square of side 2 m. Taking the point of intersection of the diagonals as the orgin the coordinates of the centre of mass are ?
View SolutionThree identical masses, each of mass 1kg, are placed at the corners of an equilateral triangle of side l. Then the moment of inertia of this system about an axis along one side of the triangle is
View Solution

