संलग्न चित्र में एक धारावाही फ्रेम ABC समबाहु त्रिभुज की आकृति में दिखाया गया है। त्रिभुज की भुजा की लम्बाई है a है तथा इसमें i ऐम्पियर का धारा प्रवाहित हो रही है । त्रिभुज के केन्द्रक O पर चुंबकीय क्षेत्र की तीव्रता ज्ञात कीजिये ।
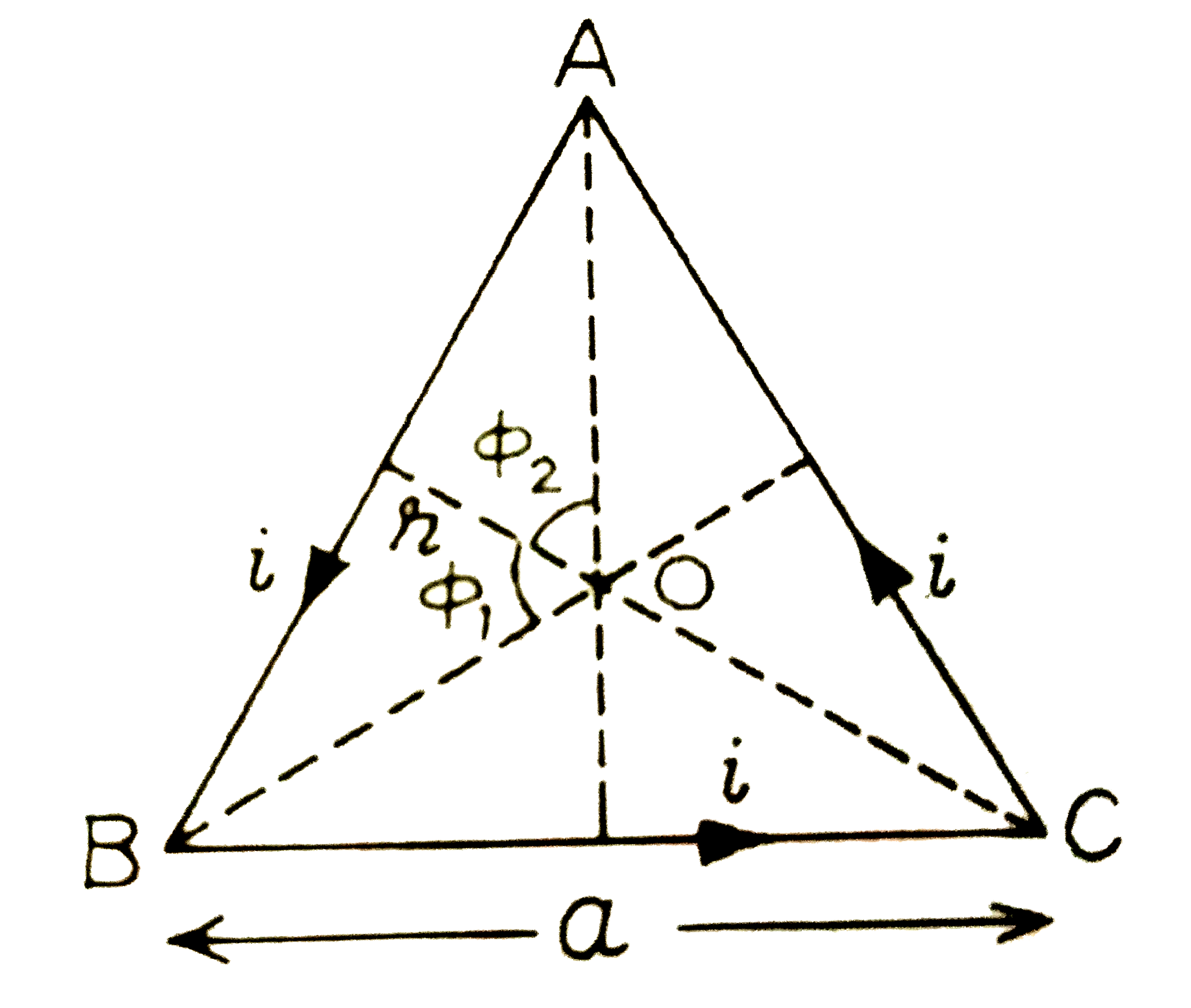
त्रिभुज के केंद्र O पर एक भुजा अब की धारा के कारण चुंबकिय क्षेत्र की तीव्रता का मान
B1=μ04πir(sinϕ1+sinϕ2)
जहाँ r,AB की Oसे लंबवत दुरी है तथा ϕ1,ϕ2 चित्रानुसार कोण है। केंद्रक O पर क्षेत्र कागज के तल के लंबवत ऊपर की ओर है। चूँकि त्रिभुज की प्रत्येक भुजा के कारण O क्षेत्रीय परिमाण व दिशा में समान है । अतः O पर परिणामी क्षेत्र का मान
B=3B1=3μ04πir(sinϕ1+sinϕ2)...(i)
समबाहु त्रिभुज में ϕ1=ϕ2=60∘
∴B=3μ04πir(√32+√32)=3√34π(μ0iπr)
परन्तु tan30∘=ra/2
∴r=a2tan30∘=a2√3
∴B=3√34×μ0iπa×√2x=9μ0i2πa
B कागज के तल लंबवत ऊपर की ओर ।
Topper's Solved these Questions
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - प्रश्नावली (वस्तुनिष्ट प्रश्न)
41 Videos
- गतिमान आवेश तथा चुंबकीय क्षेत्र BOOK - NOOTAN HINDICHAPTER - गतिमान आवेश तथा चुंबकीय क्षेत्र EXERCISE - अतिलघु उत्तरीय
84 Videos
- कॉलम का नियम तथा वैद्युत क्षेत्र BOOK - NOOTAN HINDICHAPTER - कॉलम का नियम तथा वैद्युत क्षेत्र EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
16 Videos
- चल कुण्डली धारामापी BOOK - NOOTAN HINDICHAPTER - चल कुण्डली धारामापी EXERCISE - वस्तुनिष्ठ प्रकार प्रश्न
15 Videos
Similar Questions
l लम्बाई के एक तर में i धारा प्रवाहित है । तार को मोड़ कर एक फेरे वाला वृत्तीय लूप बनाने पर, लूप के केंद्र पर उतपन्न चुंबकीय क्षेत्र B है । इस तार से 2 फेरों का लूप बनाये पर, लूप के केंद्र पर उत्पन्न चुंबकीय क्षेत्र होगा:
View Solutionबायो - सेवर्ट का नियम लिखिए तथा इसकी सहायता से विधुत धारा के S.I. मात्रक को परिभाषित कीजिए ।
View Solutionकल्पना कीजिए कि एक प्रोटॉन और एक इलेक्ट्रॉन के आवेश में अल्प अंतर होता है। इनमे से एक −e है और दूसरा(e×Δe) है। यदि एक दूसरे से 'd' दूरी पर रखे हाइड्रोजन के दो परमाणुओं के बीच (जहाँ d परमाणु के साइज से बहुत अधिक है) स्थिर वैद्युत बल और गुरुत्वीय बल का परिणामी (नैट) शून्य है तो Δe कि कोटि होगी: (दिया है हाइड्रोजन का द्रव्यमान mh=1.67×10−27kg)
View Solutionआरेख में दण्ड (छड़) चुम्बको की व्यवस्थाओं के विन्यास दर्शाये गये है। प्रत्येक चुम्बक की द्विध्रुव आघूर्ण →M है। किस विन्यास में नेट चुम्बकीय द्विध्रुव आघूर्ण का मान अधिकतम होगा?

View Solutionएक लम्बे सीधे तार में बहने वाली धारा 1 ऐम्पियर है। चुंबकीय क्षेत्र की तीव्रता 10−5 वेबर/मीटर2 होगी तार से :
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionत्रिभुज ABC की मध्याकाओं की लम्बाई ज्ञात कीजिए, जिसके शीर्ष A(3, -2), B(0, 6) और C(-2, 4) है ।
View Solutionकिसी त्रिभुज की माध्यिकाएँ …………. होती है ।
View Solutionएक त्रिभुज , जिसके शीर्ष (0,0),(0,41) तथा (41,0) है , के आंतरिक भाग में स्थित उन बिंदुओं की संख्या जिनके दोनों निर्देशांक पूर्णांक है , है :
View Solutionएक समतल निर्देशांक अक्षो को A,B,C पर इस प्रकार मिलता है की त्रिभुज ABC का केन्द्रक (1,2,3) है तो समतल का समीकरण होगा-
View Solutionएक त्रिभुज का एक शीर्ष (1,2) पर है तथा इससे होकर जाने वाली दो भुजाओं के मध्य - बिन्दु (−1,1) और (2,3) हैं , तो इस त्रिभुज का केन्द्रक है
View Solutionएक समबाहु त्रिभुज की भुजाएँ 2 सेमी/से की दर से बढ़ रही है। क्षेत्रफल के बढ़ने की दर, जबकि भुजा 10 सेमी हो, है
View Solutionकिसी वृत्त में एक चाप केन्द्र पर 45∘का कोण बनाता है। यदि चाप की लम्बाई 11 सेमी है तो वृत्त की त्रिज्या ज्ञात कीजिए।
View Solutionयदि दो समकोण त्रिभुजों में से एक त्रिभुज की एक भुजा और एक न्यूनकोण दूसरे त्रिभुज की एक भुजा और तदनुरूपी कोण के बराबर हो, तो दोनों त्रिभुज परस्पर क्या होंगे ?
View SolutionRevision |दो विशेष त्रिभुज : समबाहु तथा समद्विबाहु #!#एक त्रिभुज की दो भुजाओं की मापों का योग
View SolutionWhat is the length of the radius of the circumcircle of the equilateral triangle, the length of whose side is 6 sqrt3 cm ? एक समबाहु त्रिभुज जिसकी भुजा की लम्बाई 6 sqrt3 सेमी है, के परिवृत्त की त्रिज्या की लम्बाई कितनी होगी?
View Solution
