If $(x + 2)$ is a common factor of $(p x^{2} + q x + r)$ and $(q x^{2} + p x + r)$ then a) $p = q$ or $p + q + r = 0$ b) $p = r$ or $p + q + r = 0$ c) $q = r$ or $p + q + r = 0$ d) $p = q = - \frac{1}{2} r$

A

$| d | \leq | D |$

B

$| d | \geq | D |$

C

$| d | = | D |$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:1

$∣ ∣ p x^{2} + q x + r ∣ ∣ \leq ∣ ∣ P x^{2} + Q x + R ∣ ∣ \forall x \in R (1)$
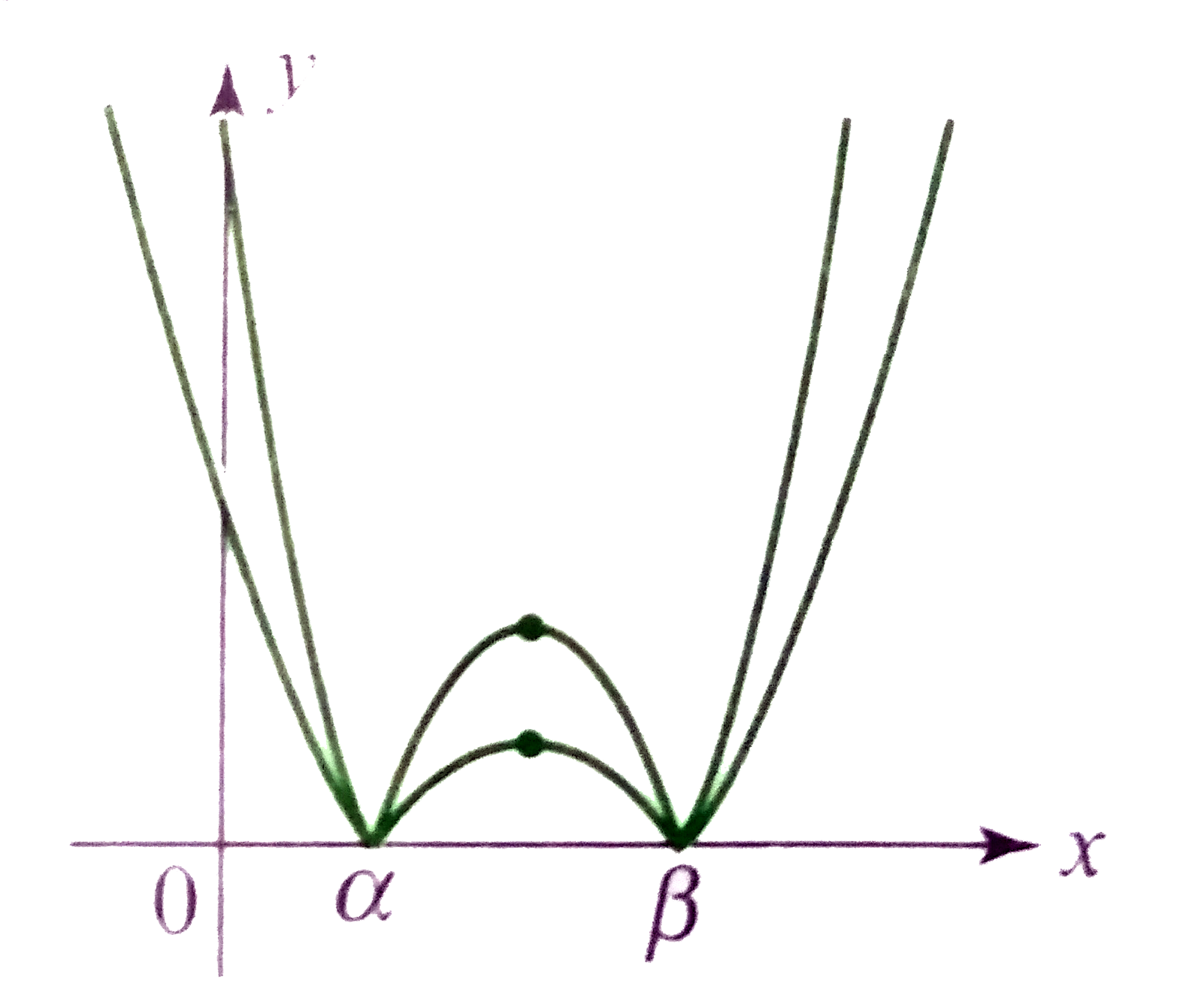
Form the graph we can see that this is possible only when both equations have same roots.
Thus, $α$ and $β$ are roots of $P x^{2} + Q x + R = 0$ and also of
$p x^{2} + q x + r = 0$
So, from (1),
$| p | | x - α | | x - β | \leq | P | | x - α | | x - β |$
$\Rightarrow | p | \leq | p |$
Also $∣ ∣ ∣ \frac{4 p r - q^{2}}{4 p} ∣ ∣ ∣ \leq ∣ ∣ ∣ \frac{4 P R - Q^{2}}{4 p} ∣ ∣ ∣$
$\Rightarrow | d | \leq ∣ ∣ ∣ \frac{p}{P} ∣ ∣ ∣ | D |$
$\Rightarrow | d | \leq | D | (∵ | p | \leq | P |)$

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

If 3 - 4i is a root of $x^{2} - p x + q = 0$ where p, q $\in R$ . then value $\frac{2 p - q}{p + q}$ is
A $- 12 / 31$
B $- 13 / 31$
C $- 15 / 31$
Dnone of these
$p^{q} - q^{r} = {(p + q)}^{r - q}$ , where $1 < q < r < p < 10$ then the value of $p + q + r$ is :
A31
B21
C15
D12

CENGAGE-THEORY OF EQUATIONS-Exercise (Comprehension)

Home
Ask Doubt
Profile