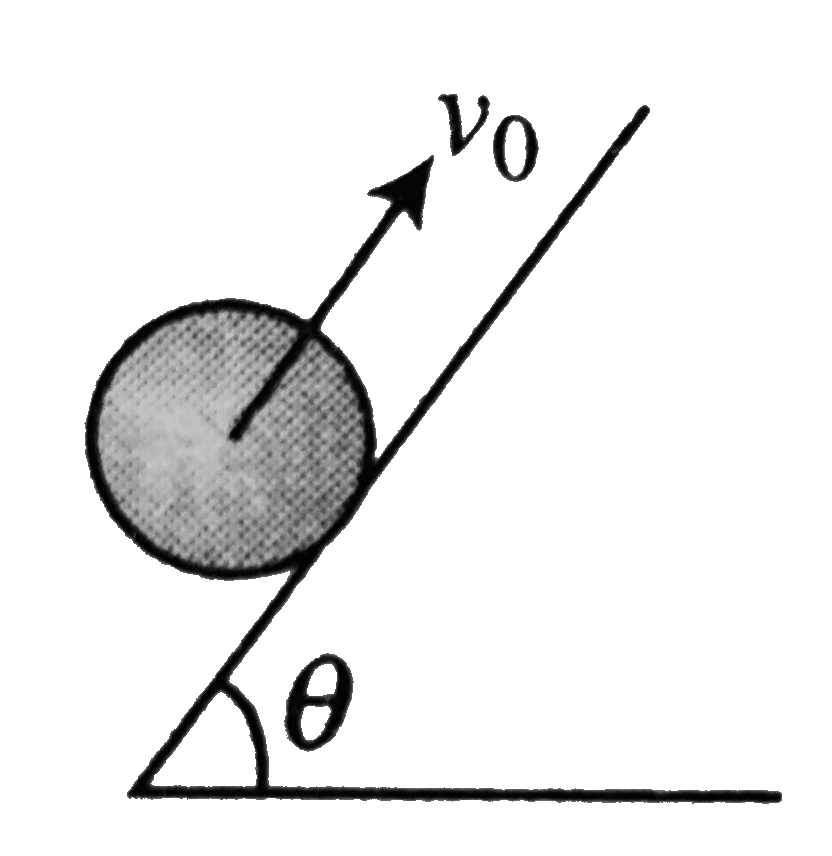
A solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is $μ = 0.5$ and radius $R$ , then find
$(a)$ Time when linear velocity becomes zero
$(b)$ Angular velocity at that instant

Video Solution

Text Solution

Verified by Experts

Velocity of lower most point is not zero hence it is not the case of pure rolling and friction is kinetic friction.
Since velocity of lower most point in forward direction therefore friction will act in backward direction.
Let retradation is a and angular retardation is $α$ .

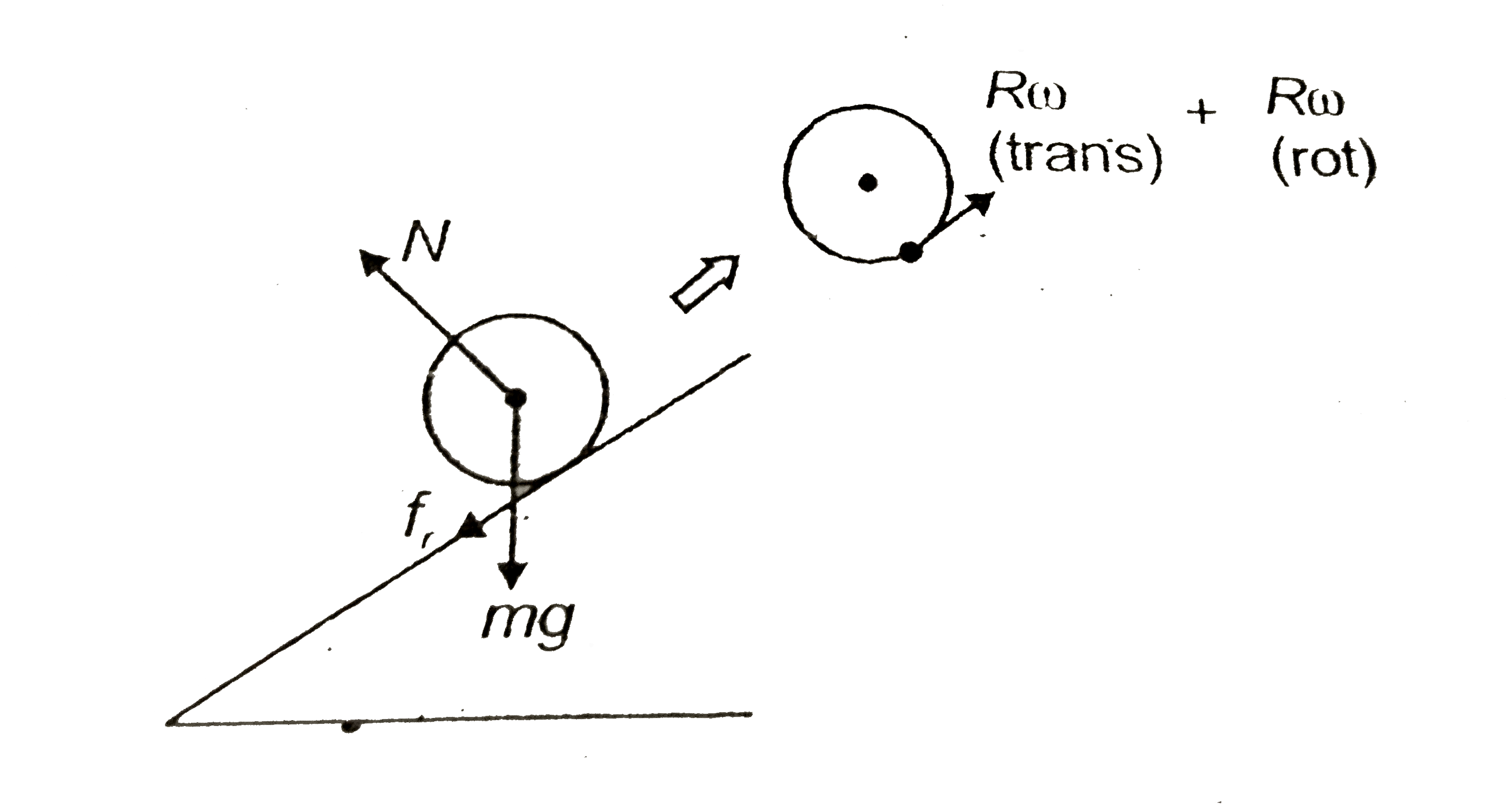
Free body diagram of sphere
$\Rightarrow m g sin θ + μ m g cos θ = m a$
$\Rightarrow a = g (sin θ + μ cos θ) = \frac{g}{\sqrt{2}} (1 + 0.5) = \frac{1.5 g}{\sqrt{2}}$ ......... $(i)$
Now
$τ$ due to friction $= R (μ m g cos θ)$
$\Rightarrow α = \frac{(μ m g cos θ)}{\frac{2}{5} m R^{2}} = \frac{5 g μ cos θ}{2 R} = \frac{5 \times 0.5 \times g \times \frac{1}{\sqrt{2}}}{2 R} = \frac{5 g}{4 R} \cdot \frac{1}{\sqrt{2}} = \frac{1.25 g}{\sqrt{2} R}$ ....... $(i i)$
For translatory moion
$V = V - a t$
$= R ω - a t$
When velocity $V$ becomes zero
$V = 0 \Rightarrow t = \frac{R ω}{a} = \frac{R ω \sqrt{2}}{1.5 g} = \frac{\sqrt{2}}{1.5} (\frac{R ω}{g})$
For rotatory motion,
$ω' = ω - α t$
$\Rightarrow t = \frac{ω}{α} = \frac{ω}{\frac{1.25 g}{\sqrt{2} R}} = \frac{R ω \sqrt{2}}{1.25 g} = \frac{\sqrt{2}}{1.25} \frac{R ω}{g}$
Linear velocity of sphere becomes zero before angular velocity become zero
Angular velocity at time $t$ when linear velocity is zero.
$ω' = ω - \frac{1.25 g}{\sqrt{2} R} \times \frac{\sqrt{2} R ω}{1.5 g}$
$\Rightarrow ω' = ω - \frac{1.25 ω}{1.5} = \frac{ω}{6}$

Updated on:21/07/2023

Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A body is projected up along a rough inclined plane of inclination $45^{\circ}$ . The coefficient of friction is 0.5. Then the retardation of the block is
A $\frac{g}{2 \sqrt{2}}$
B $\frac{g}{2}$
C $\frac{3 g}{2 \sqrt{2}}$
D $\frac{g}{\sqrt{2}}$
Question 2 - Select One or More
A sphere is projected npon a rough inclined plane. The friction coefficient between the solid sphere and the incline is $μ$ . The centre of the sphere is given an initial upward' velocity at $t = 0$ without imparting any initial angular velocity. Then, which of the following statement (s) is/are true?
APure rolling will defin!tely begin before the sphere reaches the highest point and the sphere will continue to roll purely after that, even while coming down.
BPure rolling will definitely begin before the sphere reaches the highest point but the sphere will continue to roll purely after that (even while coming down) only· if $μ$ is greater- than a certain value.
CThe sphere will be rolling purely while coming down if $μ > \frac{(2 tan α)}{7}$
DThe sphere cannot roll purely while moving up the incline
Question 3 - Select One
A solid sphere is rolling on a rough surface, whose centre of mass is at $C$ at a certain instant. Find at that instant it has angular velocity $ω$ . Its radius is $R$ . Find the angular acceleration at that instant mass of sphere is $m$

A $\frac{5}{2} \frac{g d}{R^{2}}$
B $\frac{5}{7} \frac{g d}{R^{2}}$
C $\frac{5}{2} \frac{d (g + ω^{2} R)}{R^{2}}$
D $\frac{5}{7} \frac{d (g + ω^{2} R)}{R^{2}}$

AAKASH INSTITUTE-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-Try Yourself

Home
Ask Doubt
Profile

A solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is μ=0.5 and radius R, then find (a) Time when linear velocity becomes zero (b) Angular velocity at that instant

Topper's Solved these Questions

Similar Questions

Knowledge Check

A body is projected up along a rough inclined plane of inclination 45∘ . The coefficient of friction is 0.5. Then the retardation of the block is

A sphere is projected npon a rough inclined plane. The friction coefficient between the solid sphere and the incline isμ. The centre of the sphere is given an initial upward' velocity at t=0 without imparting any initial angular velocity. Then, which of the following statement (s) is/are true?

A solid sphere is rolling on a rough surface, whose centre of mass is at C at a certain instant. Find at that instant it has angular velocity ω. Its radius is R. Find the angular acceleration at that instant mass of sphere is m

AAKASH INSTITUTE-SYSTEM OF PARTICLES AND ROTATIONAL MOTION-Try Yourself

A solid sphere is projected along an inclined plane according to diagram. If coefficient of friction is $μ = 0.5$ and radius $R$ , then find
$(a)$ Time when linear velocity becomes zero
$(b)$ Angular velocity at that instant

A body is projected up along a rough inclined plane of inclination $45^{\circ}$ . The coefficient of friction is 0.5. Then the retardation of the block is

A solid sphere is rolling on a rough surface, whose centre of mass is at $C$ at a certain instant. Find at that instant it has angular velocity $ω$ . Its radius is $R$ . Find the angular acceleration at that instant mass of sphere is $m$