Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 5 m
(ii) 20 m
(Given, density of water = 1×103kg m−3,g=10ms−2)
To find the pressure exerted below a column of water open to the atmosphere at different depths, we can use the hydrostatic pressure formula:
P=P0+ρgh
where:
- P is the total pressure at depth,
- P0 is the atmospheric pressure (approximately 1.013×105 Pascals),
- ρ is the density of the fluid (for water, ρ=1×103kg/m3),
- g is the acceleration due to gravity (given as 10m/s2),
- h is the depth in meters.
1. Identify the known values:
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=5m
2. Substitute the values into the formula:
P1=P0+ρgh
P1=1.013×105+(1×103)(10)(5)
3. Calculate the hydrostatic pressure:
P1=1.013×105+5×104
P1=1.013×105+0.5×105
P1=1.513×105Pa
Part (ii): Depth = 20 m
1. Identify the known values:
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=20m
2. Substitute the values into the formula:
P2=P0+ρgh
P2=1.013×105+(1×103)(10)(20)
3. Calculate the hydrostatic pressure:
P2=1.013×105+2×105
P2=1.013×105+2.0×105
P2=3.013×105Pa
Final Answers:
- For depth 5 m: P1=1.513×105Pa
- For depth 20 m: P2=3.013×105Pa
- P is the total pressure at depth,
- P0 is the atmospheric pressure (approximately 1.013×105 Pascals),
- ρ is the density of the fluid (for water, ρ=1×103kg/m3),
- g is the acceleration due to gravity (given as 10m/s2),
- h is the depth in meters.
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=5m
P1=P0+ρgh
P1=1.013×105+(1×103)(10)(5)
P1=1.013×105+5×104
P1=1.013×105+0.5×105
P1=1.513×105Pa
- P0=1.013×105Pa
- ρ=1×103kg/m3
- g=10m/s2
- h=20m
P2=P0+ρgh
P2=1.013×105+(1×103)(10)(20)
P2=1.013×105+2×105
P2=1.013×105+2.0×105
P2=3.013×105Pa
- For depth 5 m: P1=1.513×105Pa
- For depth 20 m: P2=3.013×105Pa
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - TRY YOURSELF
41 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTECHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTECHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
12 Videos
Similar Questions
Find the pressure exerted below a column of water, open to the atmosphere, at depth
(i) 10 m " " (ii) 30 m
(Given, density of water =1×103kgm−3,g=10ms−2)
View SolutionA glass full of water has a bottom of area 20cm2, top of area 20cm, height 20cm and volume half a litre.
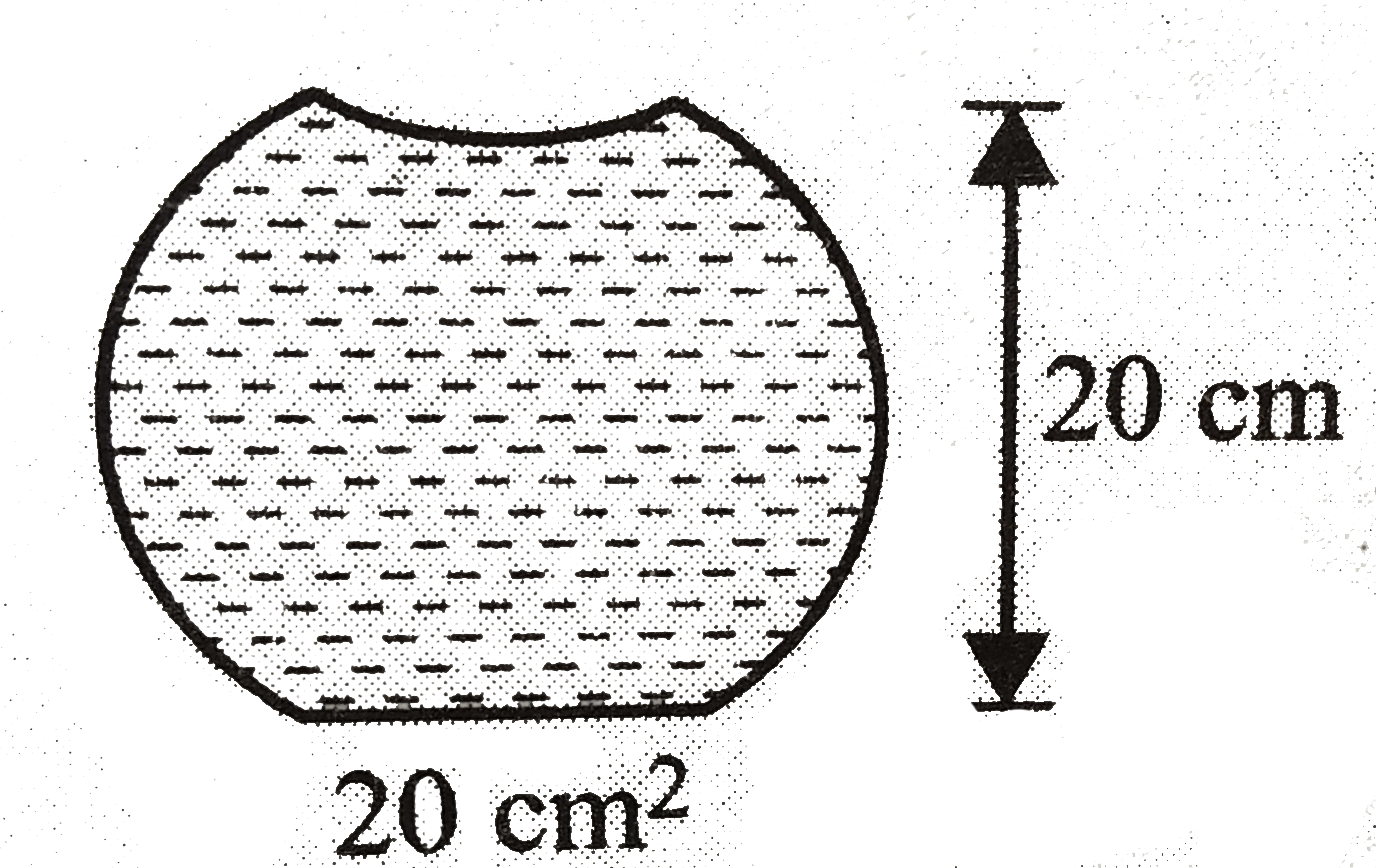
a. Find the force exerted by the water on the bottom.
b. Considering the equilibrium of the v, after. find the resultant force exerted by the side, of the glass on the water. Atmospheric pressure =1.0×105N/m2. Density of water =1000kg/m−3 and g=10m/s2
View Solution
Knowledge Check
The guage pressure exerted below a column of water, open to the earth's atmosphere at depth of 10 m is (density of water = 1000 kg/m3, g = 10 m/s2 and 1 atm pressure = 105 Pa)
A1 atmB2 atmC3 atmD4 atmThe pressure at a point in water is 10 N/m2. The depth below this point where the pressure becomes double is (Given density of water = 103 kg m−3, g = 10 m s−2)
A1 mmB1 cmC1 mD10 cmA body is experiencing an atmospheric pressure of 1.01×105N/m2 on the surface of a pound . The body will experience double of the previous pressure if it is brought to a depth of (given density of pound water =1.03×103kg/m2,g=10m/s2 )
A8 mB8 . 6 mC9 . 7 mD10 . 3 m
The pressure acting on a submarine is 3×105 at a certain depth. If the depth is doubled the percentage increase in the pressure acting on the submarine would be :
(Assume that atmospheric pressure is 1×105 Pa density of water is 103kgm−3,g−10ms−2)
View SolutionCalculate the total pressure at the bottom of a lake of depth 5.1 m (atm pressure =105 P), density of water =103kg/m3,g=10m/s2
View SolutionA vessel full of water has a bottom of area 20cm2, top of area 20cm2, height 20 cm and volume half a litre as shown in figure.
(a) find the force exerted by the water on the bottom.

(b) considering the equilibrium of the water, find the resultant force exerted by the sides of the glass vessel on the water. atmospheric pressure =1.0×105N/m2. density of water =1000kg/m3 and g=10m/s2
View SolutionA body is experiencing an atmospheric pressure of 1.01×105N/m2 on the surface of a pond. The body will experience double of the previous pressure if it is brought to a depth of (given density of pond water =1.03×103kg/m2, g=10m/s2)
View SolutionA body is experiencing an atmospheric pressure of 1.01×106N/m2 on the surface of a pound. The body will experience double of the previous pressure if it is brought to a depth of (given density of pound water =1.03×103kg/m2,g=10m/s2)
View Solution
