A light spring is loaded with a mass under gravity . If the spring extends by 10cm ,calculate the period of small vertical osciallation.
0.628s
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-J )8videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - EXAMPLE21videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-H ( MULTIPLE TRUE-FALSE TYPE QUESTIONS) )3videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)5videos
PHYSICAL WORLD
Similar Questions
In the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.
 View Solution
View SolutionA steel sprial spring has on unstreched length of 8cm and when a mass is hung o it, its length becomes 10cm. Calculate the periodic time of the oscillation that would occur if the masss were displaced vertically.
View Solution
Knowledge Check
- Question 1 - Select One
Two identical springs are attached to a small block P. The other ends of the springs are fixed at A and B, When P is in equilibrium the extension of bottom spring is 10 cm. The period of small vertical oscillations of P about is equilibrium position is (useg=9.8m/s2)
 A2π7secBπ7secC2π5secDnone of these
A2π7secBπ7secC2π5secDnone of these - Question 2 - Select One
Two identical spring are attached to a small block P The other ends of the springs are fixed at A and B. when P is equilibrium the extension of top spring is 20cm and extension of bottom spring is 10cm The period at small vertical oscillation of p about its equilibrium position is (use g=9.8m/s2)
 A2π7secBπ7secC2π5secDnone of these
A2π7secBπ7secC2π5secDnone of these - Question 3 - Select One
A spring has a certain mass suspended from it and its period for vertical oscillation is T. The spring is now cut into two equal halves and the same mass is suspended from one of the halves. The period of vertical oscillation is now
AT2BT√2C√2TD2T

In the arrangement shown if Fig. Pulleys are small and light and spring are ideal and K1=25(π2)Nm, K2=2K1,K3= and K4=4K1 are the force constant of the spring. Calculate the period of small vertical oscillation of block of mass m=3kg.View SolutionPeriodic time of oscillation T1 is obtained when a mass is suspended from a spring if another spring is used with same mass then periodic time of oscillation is T2. Now if this mass is suspended from series combination of above spring then calculate the time period.
View SolutionIn the arrangement shown in the diagram, pulleys are small and springs are ideal. k1=k2=k3=k4=10Nm−1 are force constants of the springs and mass m=10kg. If the time period of small vertical oscillations of the block of mass m is given by 2πx seconds, then find the value of x.
 View Solution
View SolutionA body of weight 30N hangs from one end of a long, vertical spring whose other end is attached to a rigid support. The spring extends by 5cm when a force of 10N is applied to it. The time period of the vertical oscillations of the body is
View SolutionTwo identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
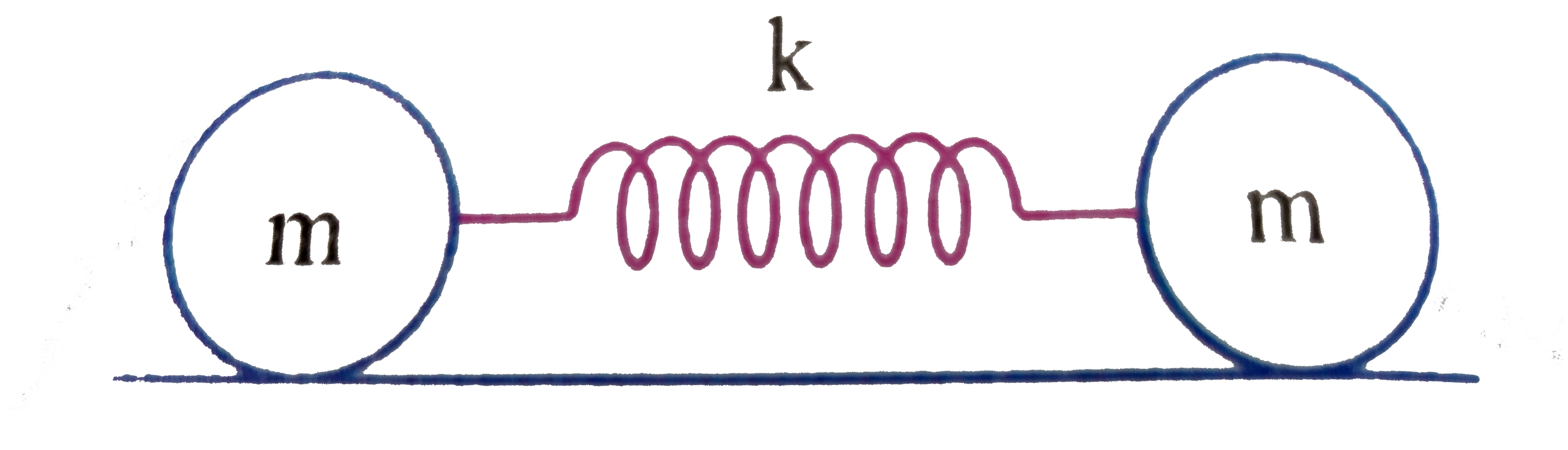 View Solution
View Solution

