As a result of adding two mutually perpendicular oscillations of equal frequency the motion of an object occurs alongan ellipse, in one case the motion is clockwise, while in the other it is counter clockwise . Write the equations of motion along each coordinate axis, assuming that the initial phase along the x-axis is zero.
x= A_(x) sin omegat , y = A_(y) sin (omegat + (pi)/(2))forclockwise<br>x= A_(x)sin omega t , y = A _(y) sin (omegat - ( pi)/(2)) for counter clockwise
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
21 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Exercise
20 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
7 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
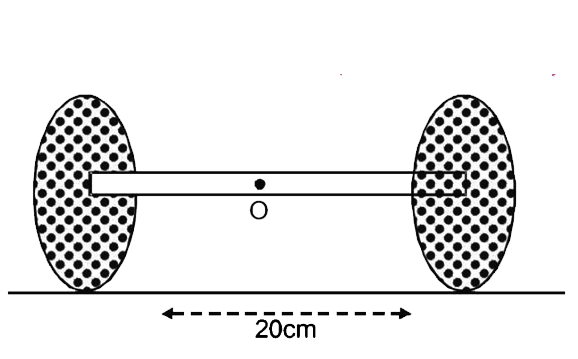
Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.
View SolutionTwo boats A and B moved away from a buoy anchored in the middle of a river along the mutually perpendicular straight lines. A moved along the river and B at fight angle to it Having moves off equal destances from the boy, the boats returned. Find the ratio of the times of motion of the boats, if the velocity of each boat with rspect to still warer in η times greater than the velocity of warer current.
View Solution
Knowledge Check
An object is moving with uniform acceleration a. Its initial velocity is u and after time t its velocity is v. The equation of its motion is v = u + at. The velocity (along y-axis) time (along x-axis) graph shall be a straight line
Apassing through originBwith x-intercept uCwith y-intercept uDwith slope uThe equation describing the motion of a simple harmonic oscillator along the X axis is given as x=Acos(ωt+ϕ). If at time t = 0, the oscillator is at x = 0 and moving in the negative x direction, then the phase angle ϕ is
Aπ2B−π2CπD0Two simple harmonic motions with the same frequency act on a particle at right angles i.e., along X-axis and Y-axis. If the two amplitudes are equal and the phase difference is π/2, the resultant motion will be
Aa circleBan ellipse with the major axis along Y-axisCan ellipse with the major axis along X-axisDa straight line inclined at 45∘ to the X-axis
Two thin circular disks of mass 2kg and radius 10 cm each are joined by a rigid massless rod of length 20 cm. the axis of the rod is along the perpendicular to the planes of the disk through their centres. This object is kept on a truck in such a way that the axis of the object is horizontal and perpendicular to the direction of the motion of the truck. Its friction with the floor of the truck is large enough so that the object can roll on the truck without slipping. Take x axis as the direction of motion of the truck and z-axis as the vertically upwards direction. if the truck has an acceleration of 9m/s2 Calculate:
(i) The force fo friction on each disk,
(ii) The magnitude and the direction of the frictional torque acting on each disk about the centre of mass O of the object. Express the torque in the vector form in terms of unit vectors ˆi,ˆjandˆk in the x,y, and z directions.

View SolutionConsider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
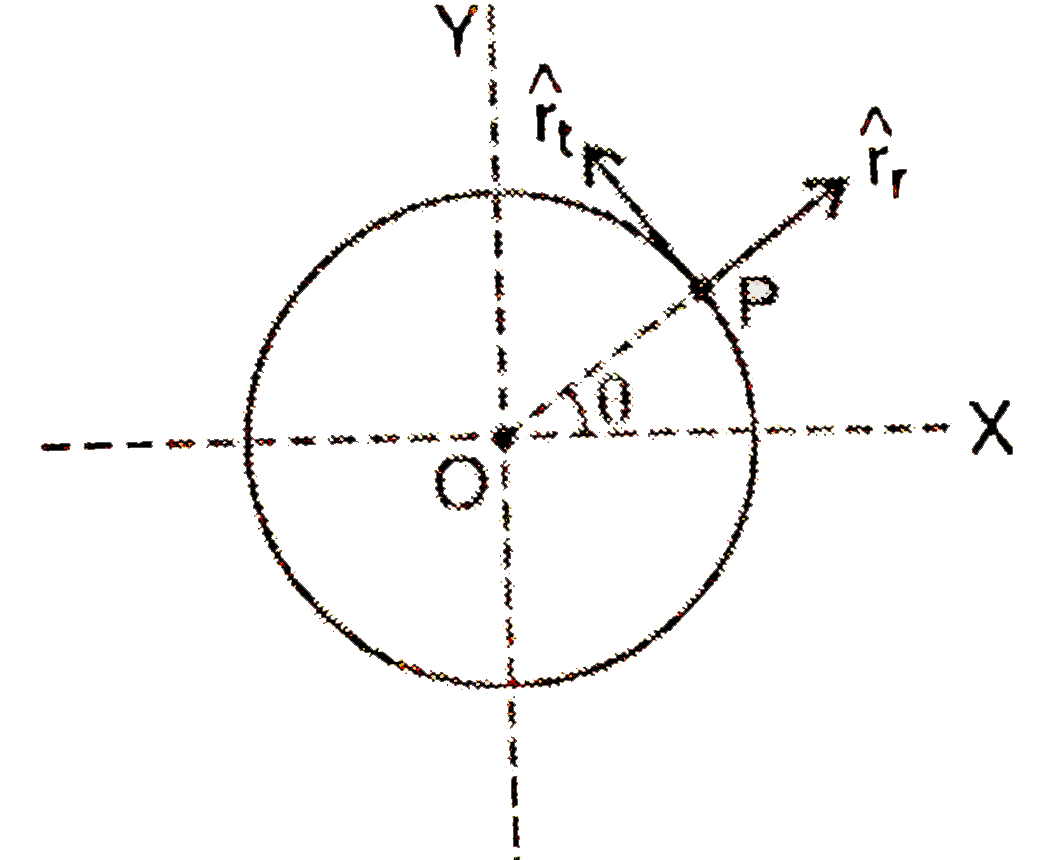
Answer the following questions :
For any instantantaneous position of the objected P, the radial unit vector ˆrr can be expressed as :
View SolutionConsider a point object of mass 'm' moving in a circle of radius a=1m. For any instantaneous position of the object, θ is the angle that the radial line joining the object and the centre makes with the position X-axis of a cartesian coordinate system with the centre of circle O as the origin. ˆi and ˆj are unit vectors along X- axis and Y-axis, respectively . Suppose that the motion is a 'Unifrom Circular Motion ' with a constant angular speed π36rad/sec and that the sense of rotation is counterclockwise with θ=0att=0 . For an object which moves in a circle , it is usually convenient to introduce two mutually perpendicular unit vectors ˆrr and ˆrt, as shown in the fig 3.57. Here ˆrr is the radial unit vector and ˆrt , the tangential unit vector.
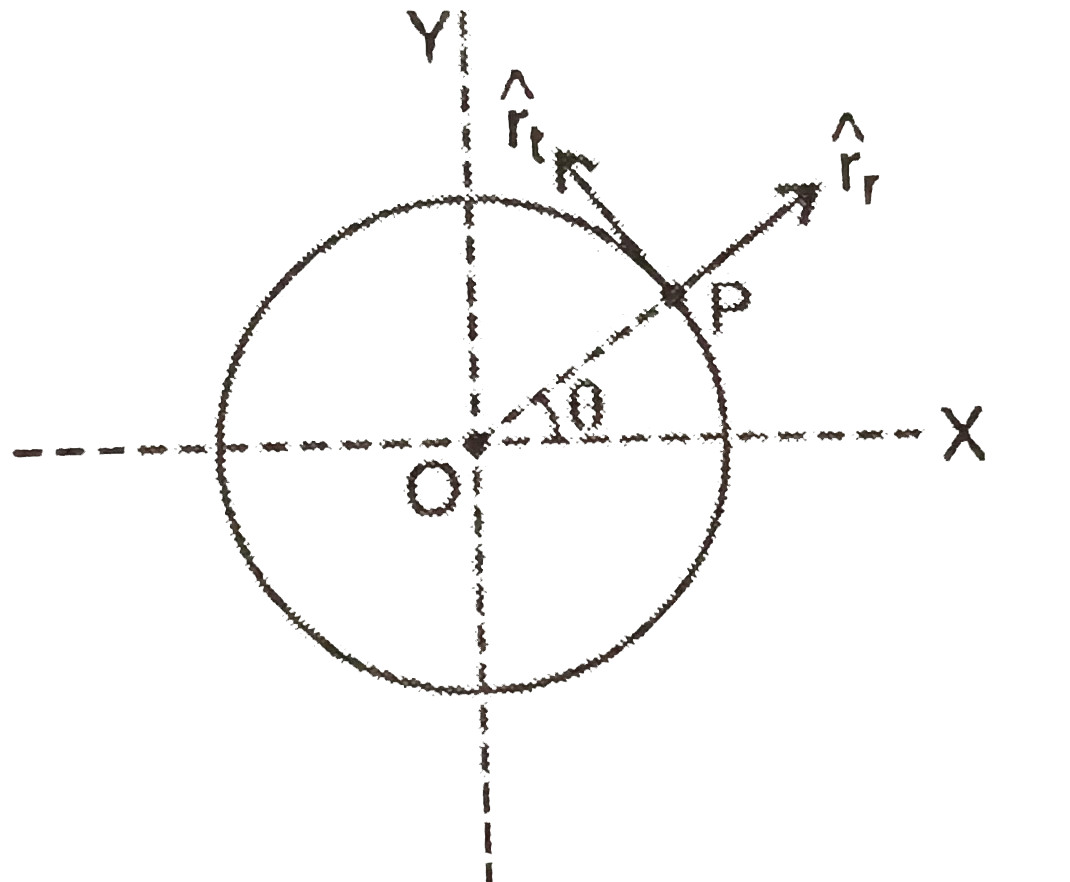
Answer the following questions :
For any position of the objected P, the tangential unit vector can be expressed as :
View SolutionTwo circular coils mounted parallel to each other on the same axis carry steady currents. If an observer between the coils reports. that one coil is carrying a clockwise current i1 While the other is carrying a counter - clockwise current i2 then the two coils experience
View SolutionTwo S.H.M.s along the same straight line in the same direction and of the same period are given by the equations, x1=3 sin(4πt+π6) and x2=4 sin(4πt+π3). The initial phase of the resultant motion is
View Solution