A ball of mass, m is attractive to two springwhich are already stretched so that each pulls on to ball with a force F. length of each spring . In this Determine the period of small oscillations of the ball in a difference perpendicular of length of psirng. Difference of the mass of spring and gravity .

T=2π√ml2F
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - EXAMPLE
21 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - Exercise
20 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-I(SUBJECTIVE TYPE QUESTIONS) )
7 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
figure shown a partical mass m=100g attaches with four identical spring , each of length l=10cm . Initial tension in each spring is F0=25N. Neglecting gravity , Calculate the period of small oscillation of the article along a line perpendicular to the plane of the figure .

View SolutionFigure shows a particle mass m=100g attaches with four identical spring , each of length l=10cm . Initial tension in each spring is F0=25N. Neglecting gravity , Calculate the period of small oscillation of the particle along a line perpendicular to the plane of the figure .

View Solution
Knowledge Check
The following figure shows a particle of mass, m, attached with four identical springs, each of length l. Initial tension in each spring is F0. The period of small oscillations of the particle along a line perpendicular to the plane of the figure is (neglect gravity)
 Aπ√mlF0B2π√mlF0C2π√ml2F0Dπ√ml4F0
Aπ√mlF0B2π√mlF0C2π√ml2F0Dπ√ml4F0In the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.
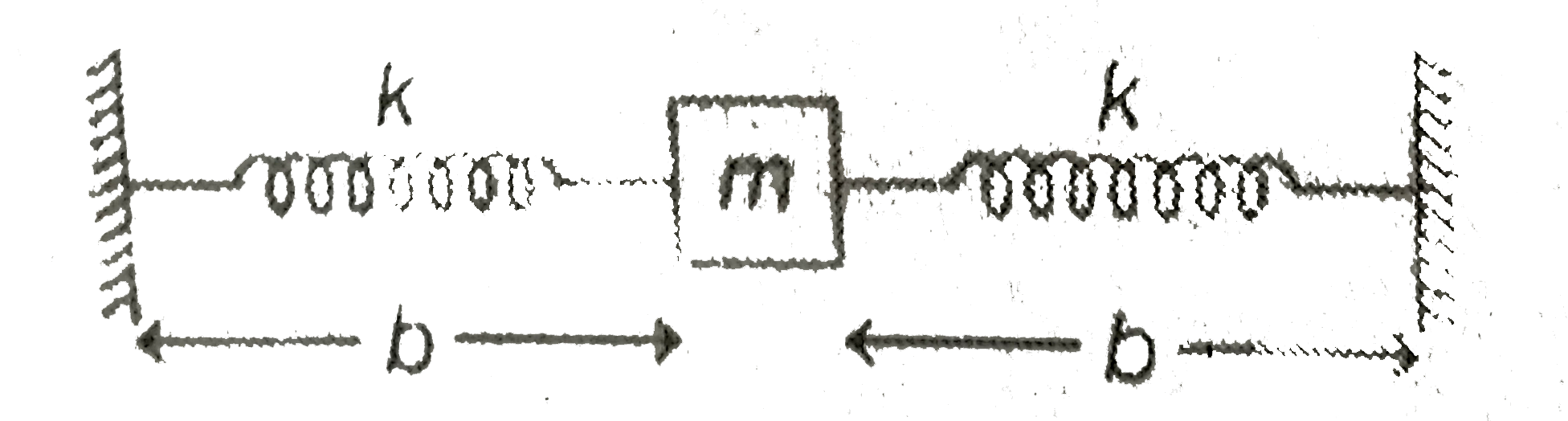 A2π√mbk(b−1)B2π√mb2k(b−l)C2π√(mb−lkb)D2π√(mb−l2kb)
A2π√mbk(b−1)B2π√mb2k(b−l)C2π√(mb−lkb)D2π√(mb−l2kb)Two identical particles each of mass 0.5kg are interconnected by a light springs of stiffness 100N/m, time period of small oscillation is ….
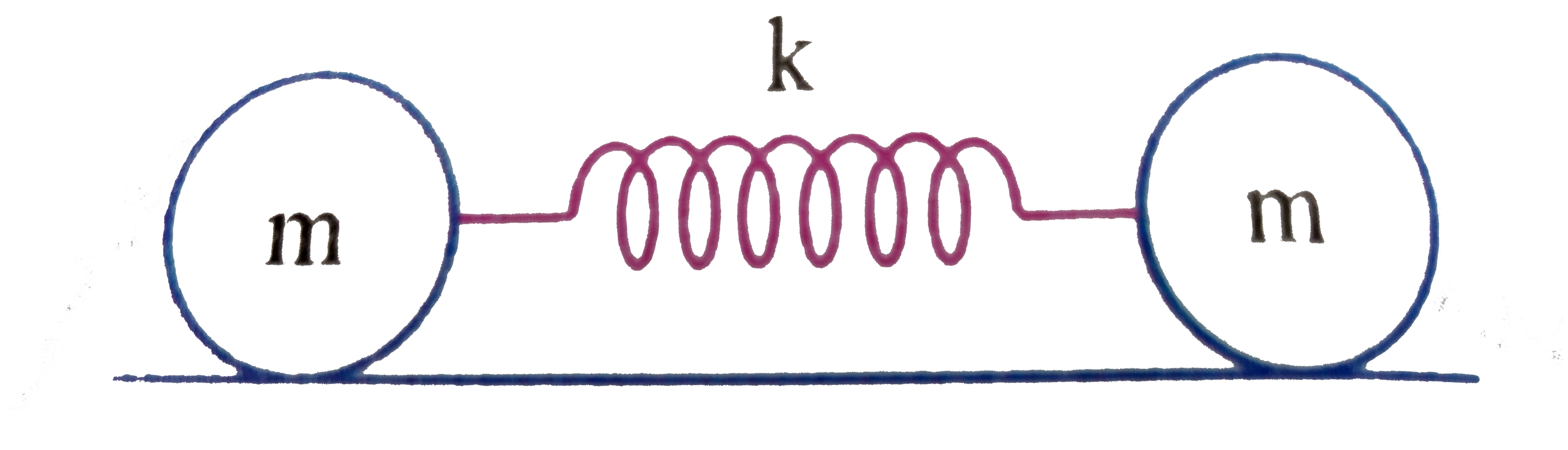 Aπ5√2Bπ10√2sCπ5sDπ10s
Aπ5√2Bπ10√2sCπ5sDπ10s
In the figure, a block of mass m is rigidly attached to two identical springs of stiffness k each. The other ends of the springs are connected to the fixed wall. When the block is in equilibrium, length of each spring is b, which is greater than the natural length of the spring. The time period of the oscillation of the block if it is displaced by small distance perpendicular to the length of the springs and released. Space is gravity free.

View SolutionA ball of mass m is attached to a light string of length L and suspended vertically. A constant horizontal force, whose magnitude F equals the weight of the ball, is applied Determine the speed of the ball as it reaches the 90∘ level.
View SolutionA ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionA ball of mass m kept at the centre of a string of length L is pulled from centre in perpendicular direction and released. Prove that motion of ball is simple harmonic and determine time period of oscillation
View SolutionOn a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant k, the period of oscilation of the body is (assuming the spring as massless)
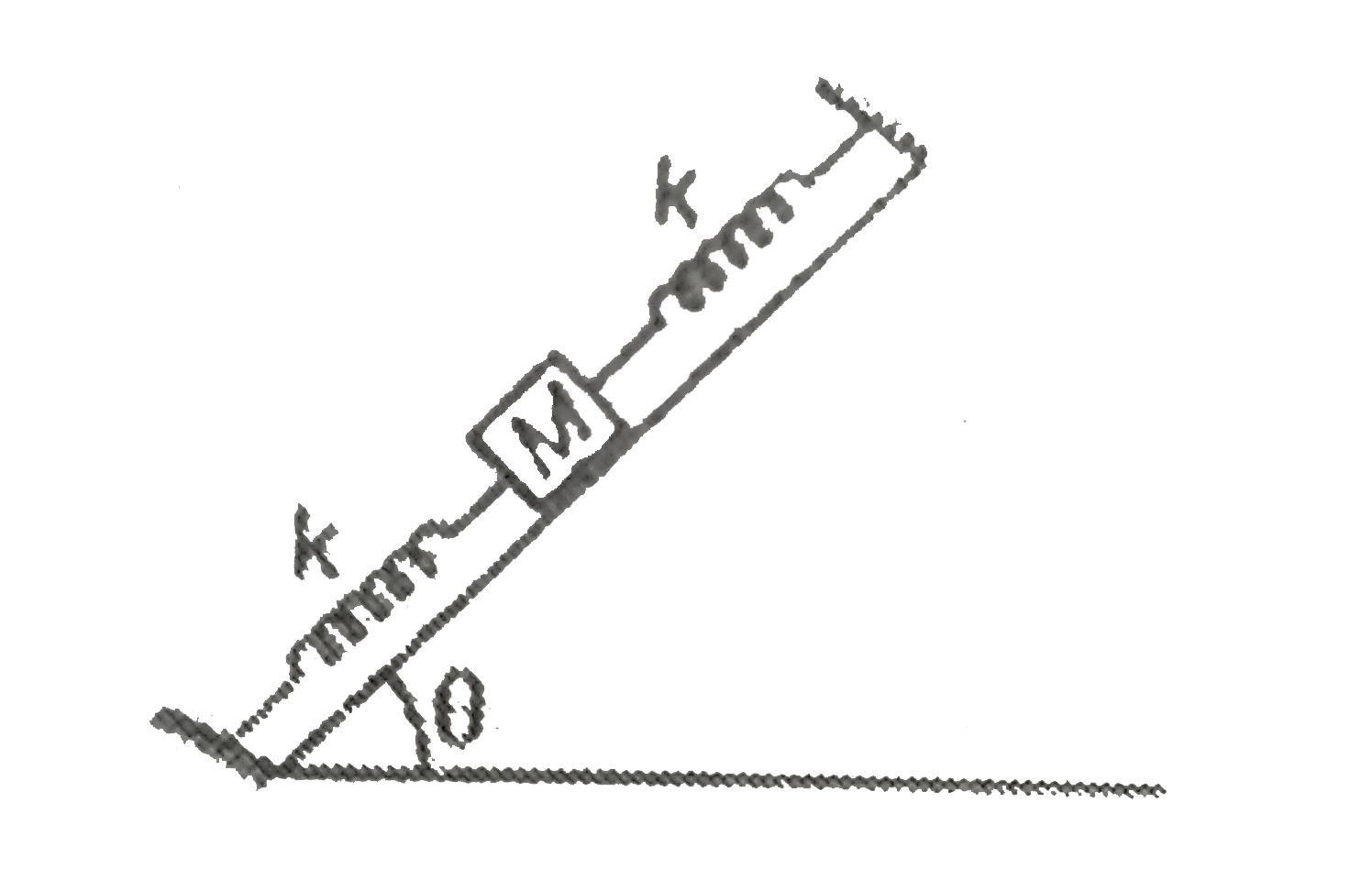
View Solution
