The values of apparent angles of dip in two places measured in two mutually perpendicular planes are $30^{\circ}$ and $45^{\circ}$ . Determine the true angle of dip at the place

Video Solution

Text Solution

Verified by Experts

Let $ϕ$ be the true angle of dip and $ϕ_{1}, ϕ_{2}$ be the apparent angles of dip in two mutually perpendicular planes such that $ϕ_{1} = 30^{\circ}$ and $ϕ_{2} = 45^{\circ} ϕ = ?$
Consider the figure shown below

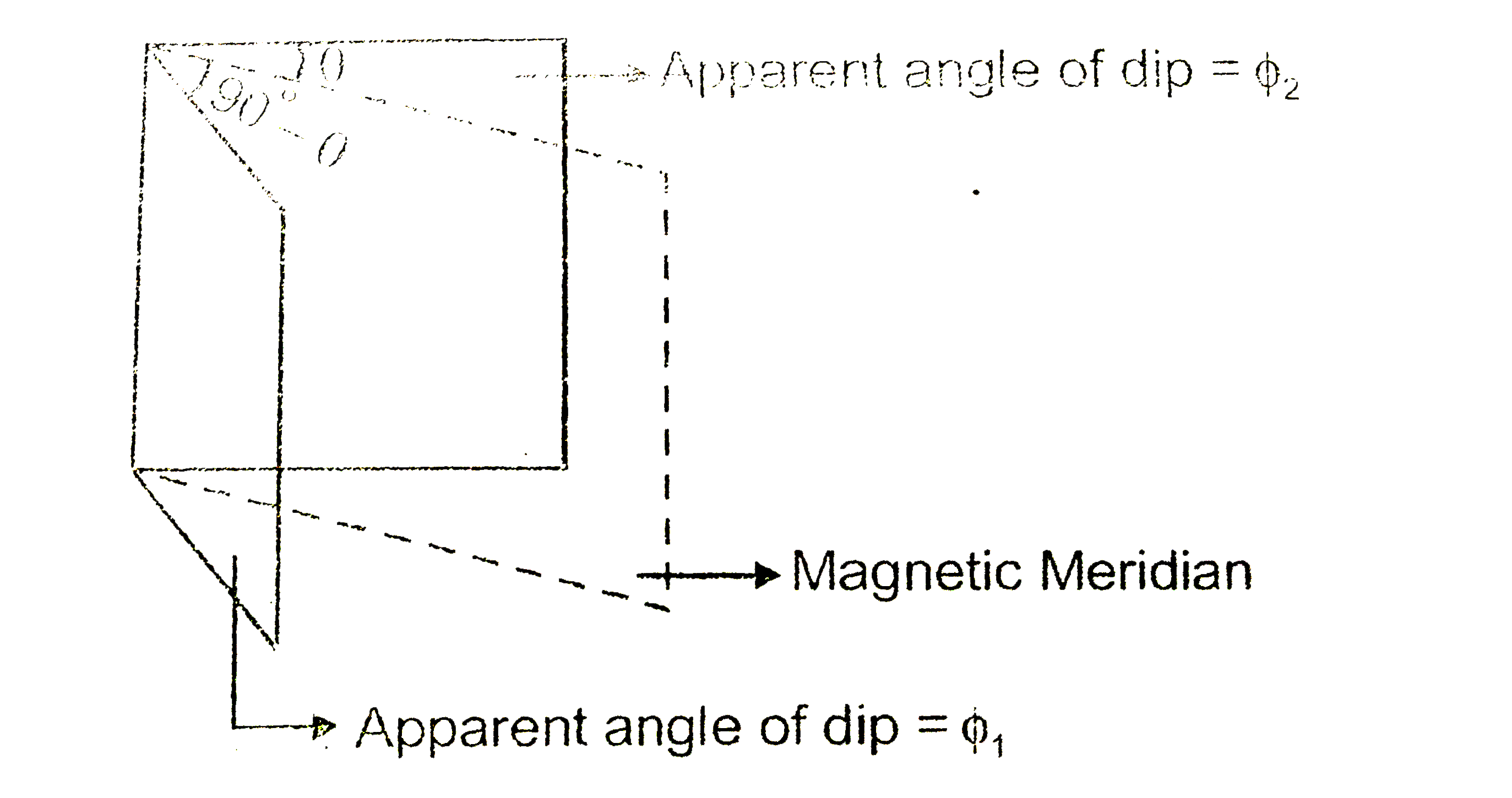
If one vertical plane is at angle $θ$ with magnetic meridian , the other vertical plane makes angle $90^{\circ} - θ$ with the magnetic meridian .
The apparent angle of dip is related to true angle of dip as
$tan ϕ' = \frac{tan ϕ}{cos θ}$
So, we can write
${tan ϕ}_{1} = \frac{tan ϕ}{cos θ} ... (i)$
and ${tan ϕ}_{2} = \frac{tan ϕ}{sin θ} ... (i i)$
As we know that
${sin}^{2} θ + {cos}^{2} θ = 1$
So , we get
$\frac{{tan}^{2} ϕ}{{tan}^{2} ϕ_{1}} + \frac{{tan}^{2} ϕ}{{tan}^{2} ϕ_{2}} = 1$
$\Rightarrow {cot}^{2} ϕ_{1} + {cot}^{2} ϕ_{2} = {cot}^{2} ϕ$
Plugging in the values of $ϕ_{1}$ and $ϕ_{2}$ , we get
${cot}^{2} 30^{\circ} + {cot}^{2} 45^{\circ} = {cot}^{2} ϕ$
$\Rightarrow {cot}^{2} ϕ = 3 + 1$
= 4
$cot ϕ = 2$
$ϕ = {cot}^{- 1} (2)$
= $\frac{{tan}^{- 1} (1)}{2}$ .

The values of the apparent angles of dip in two planes at right angles to each other are $30^{\circ}$ and $45^{\circ}$ . Then the true value of the angle of dip at the place is
A ${tan}^{- 1} 1$
B ${tan}^{- 1} 2$
C ${cot}^{- 1} 2$
D ${cot}^{- 1} 1$
The values of the apparent angles of dip in two planes at right angles to each other are $30^{\circ}$ and $45^{\circ}$ . Then the true value of the angle of dip at the place is
A ${cot}^{- 1} (1)$
B ${cot}^{- 1} (2)$
C ${cot}^{- 1} (3)$
D ${cot}^{- 1} (4)$
The values of apparent angles of dip in two places measured in two mutually perpendicular planes are $30^{\circ}$ and $45^{\circ}$ . Determine the true angle of dip at the place
A ${tan}^{- 1} (2)$
B ${tan}^{- 1} (\frac{1}{2})$
C ${tan}^{- 1} (\sqrt{2})$
D $60^{\circ}$