Ifp>q>0andpr<−1<qr, then find the value of tan−1(p−q)1+pq+tan−1(q−r)1+qr+tan−1(r−p)1+rp.
0
−π
π
π2
The correct Answer is:C
Step by step video, text & image solution for Ifp > q >0a n dp r<-1<q r , then find the value of tan^(-1)(p-q)/(1+p q)+tan^(-1)(q-r)/(1+q r)+tan^(-1)(r-p)/(1+r p)dot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - C)(OBJECTIVE TYPE QUESTIONS (MORE THAN ONE OPTIONS ARE CORRECT))13videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - D)(LINKED COMPREHENSION TYPE QUESTIONS)9videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - ASSIGNMENT (SECTION - A)(OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT))45videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTECHAPTER - INTEGRALSEXERCISE - Try yourself50videos
INTEGRALS
- BOOK - AAKASH INSTITUTECHAPTER - LIMITS AND DERIVATIVES EXERCISE - Section - j3videos
LIMITS AND DERIVATIVES
Similar Questions
If p>qandr<0 , then which is true? (a) pr < qr (b) p r < q r (c) p + r < q + r (d) None of these
View SolutionIf a,bandc are in A.P., and pandp' are respectively, A.M. and G.M. between aandbwhileq,q' are , respectively, the A.M. and G.M. between bandc, then p2+q2=p'2+q'2 b. pq=p'q' c. p2−q2=p'2−q'2 d. none of these
View Solution
Knowledge Check
- Question 1 - Select One
If rthand(r+1)th terms in the expansion of (p+q)n are equal, then (n+1)qr(p+q) is
A12B14C1D0 - Question 2 - Select One
If roots of the equation (q−r)x2+(r−p)x+(p−q)=0 are equal, then p,q and r are in
AAPBGPCHPDAGP
If P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
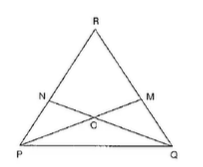
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
 View Solution
View SolutionIf p, q, r are not in G.P. and ∣∣ ∣ ∣∣1qpα+qp1rpα+rqpα+qqα+r0∣∣ ∣ ∣∣=0 Show that pα2+2qα+r=0
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
 View Solution
View SolutionIf rth and (r+1)th term in the expansion of (p+q)n are equal, then (n+1)qr(p+q) is
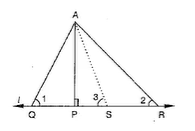
View SolutionIn Figure, AP ⊥l and PR>PQ . Show that AR>AQ Given: AP⊥l and PR>PQ To Prove: AR>AQ Construction: Mark a point S on PR such that PS=PQ. Join AS
 View Solution
View Solution

