
In the above figure,the circles with centres P,Q and R intersect at point B,C,D and E as shown. Lines CB and ED intersect in point M. Lines drawn from point M touch the circles at points A and F. Prove that MA = MF.
In circle with centre P, MA is a tangent and MC is a secant.
∴MA2=MB×MC …(Tangent secant segments theorem)
In circle with centre Q,MC and ME are secant
∴MB×MC=MD×ME… (Theorem of external division of chords) ….(II)
In circle with centre R, MF is a tangent and ME is a secant.
∴MF2=MD×ME ... (Tangent secant segments theorem)
∴MA2=MF2.... (From I, II and III)
∴MA=MF ....(Taking square root)
Topper's Solved these Questions
- MODEL QUESTION PAPERBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MODEL QUESTION PAPERExercise:SOLVE THE FOLLOWING SUBQUESTIONS: (ANY ONE)
Explore 2 Videos
- MODEL QUESTION PAPERBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MODEL QUESTION PAPERExercise:SOLVE ANY TWO OF THE FOLLOWING SUBQUESTIONS:
Explore 4 Videos
- MENSURATIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MENSURATIONExercise:Assignment 8.5
Explore 8 Videos
- PRACTICE QUESTION BASEDBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:PRACTICE QUESTION BASEDExercise:STATISTICS
Explore 13 Videos
Similar Questions
In the figure, two circles with centers O and P intersect each other at points D and C. Line AB intersects the circle with centre O at points A and B and touches the circle with centre P at point E. Prove ∠ADE+∠BCE=180∘.

View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.

View SolutionLine and Circle have No Intersection Point.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
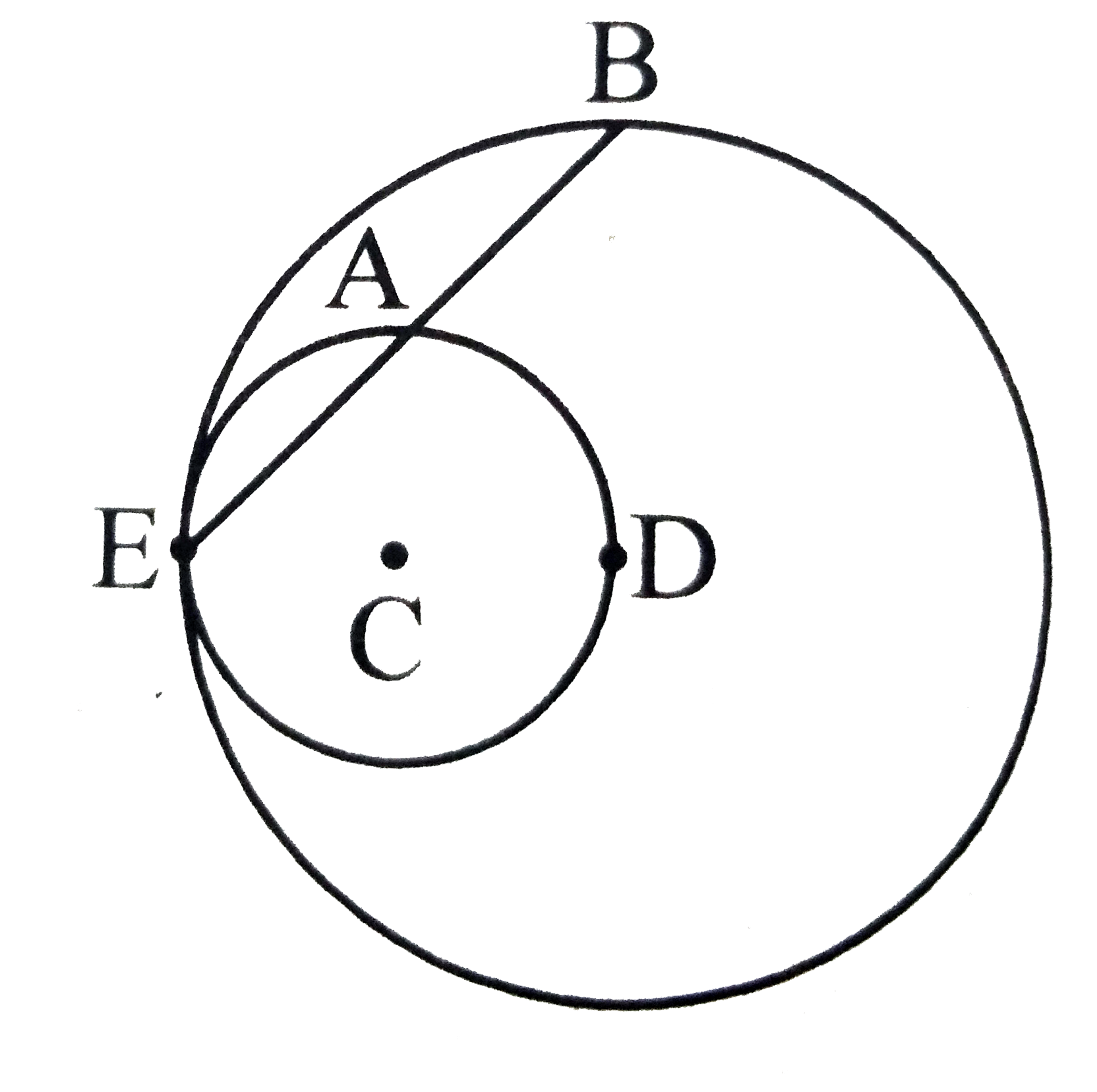
View SolutionIn the adjoining figure , circles with centres C and D touch internally at point E. D lies on the inner circle. Chord EB of the other circle intersects innet circle at point A. Prove that, seg EA≅seg AB.
View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
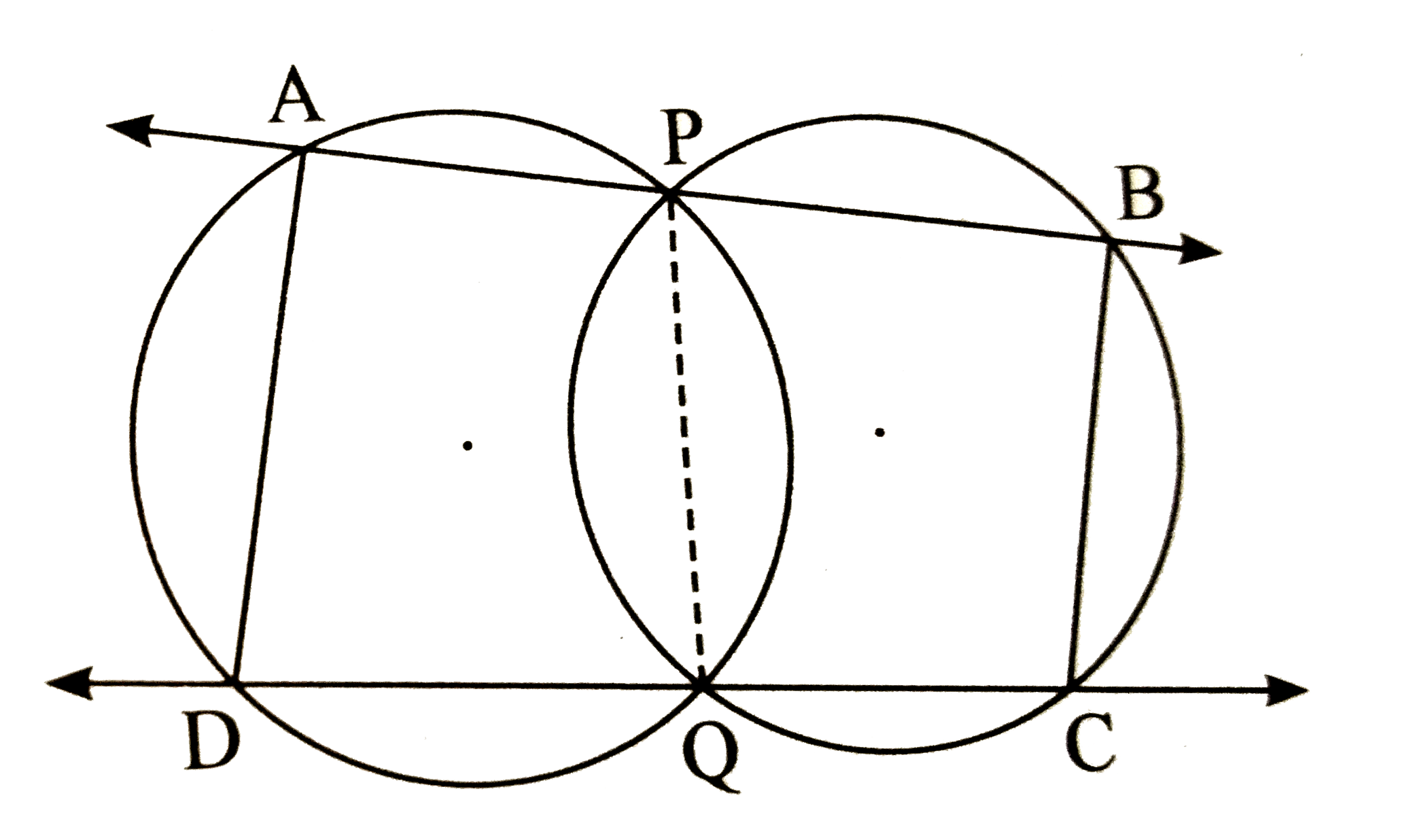
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

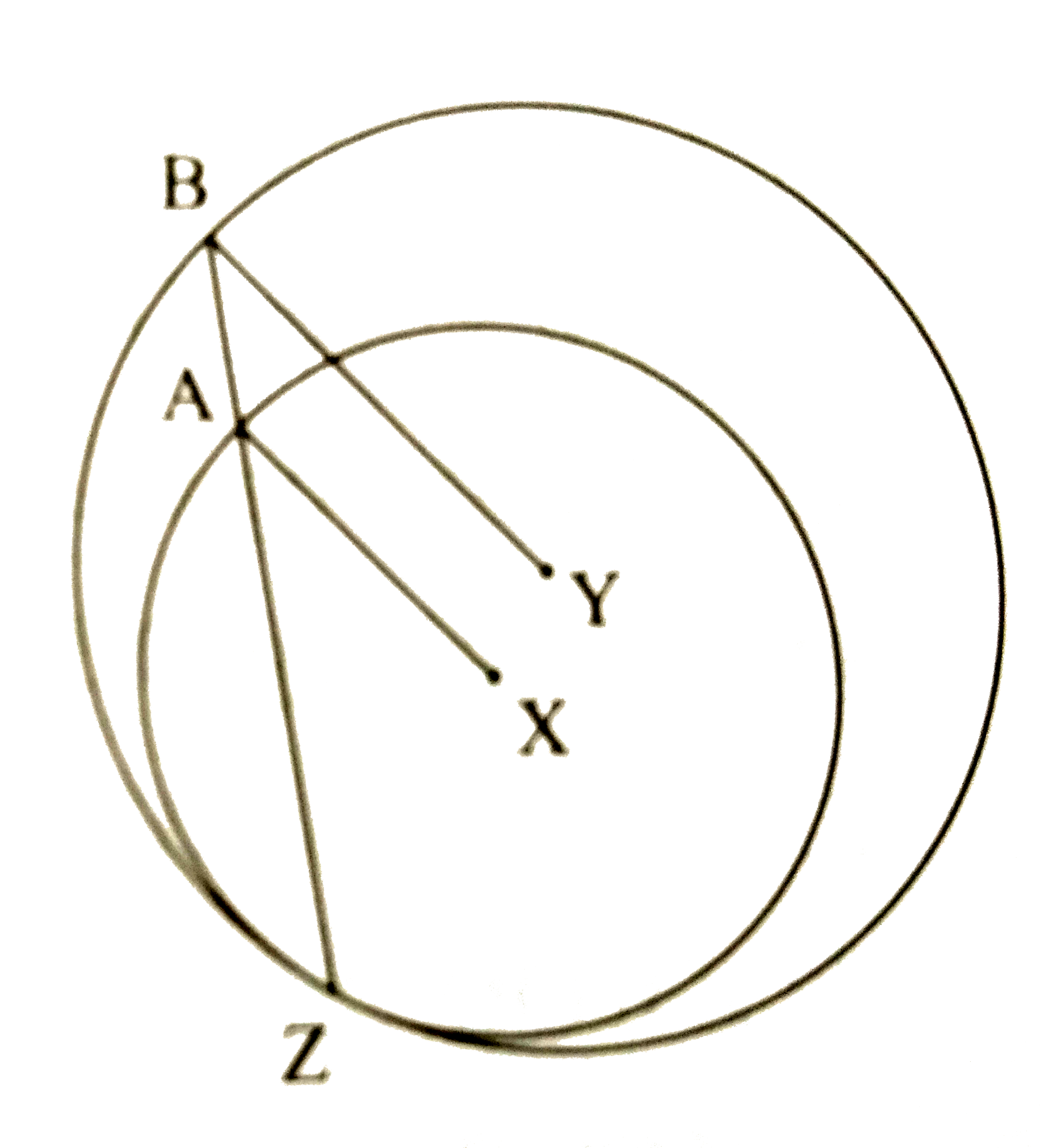
View SolutionIn the figure, circles with centres X and Y touch internally at point Z. Seg BZ is a chord of bigger circle and it intersects smaller circle at point A. Prove that, seg AX || seg BY.
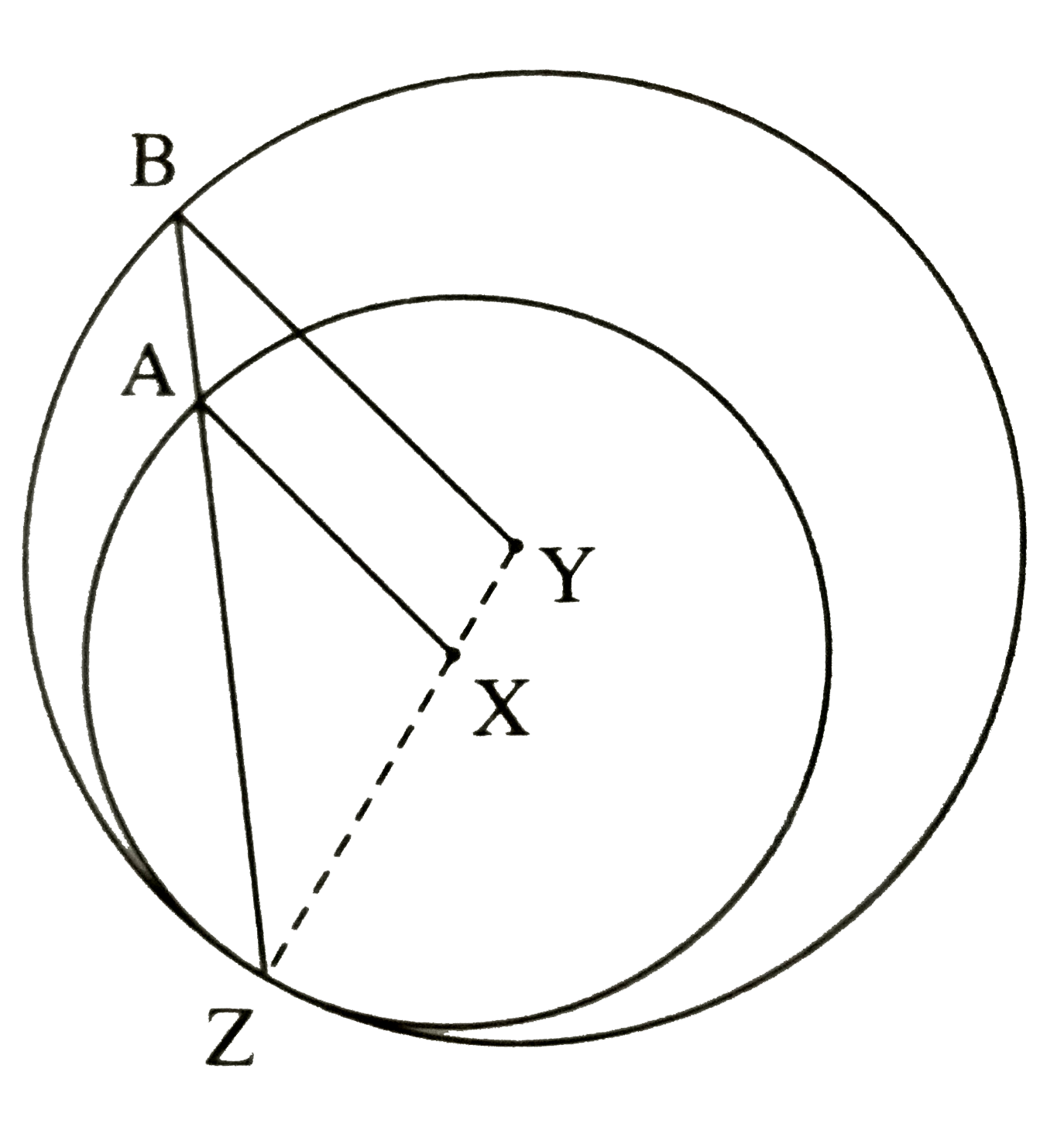
View SolutionIn the figure , circles with centres X and Y touch internally at point Z. Seg BZ is the chord of bigger circle and it intersects smaller k circle at point A.
Prove that seg AX∣∣ seg BY.
View SolutionIn figure, circles with centers C and D touch internally at point E. D lies on the inner circle. Chrd EB of the outer circle intersects inner circle at point A. Prove that, seg EA ≅ seg AB.

View Solution